Fluid flow past a cylinder: Difference between revisions
imported>Brian Fiedler No edit summary |
imported>Brian Fiedler |
||
| Line 3: | Line 3: | ||
== Mathematical Solution == | == Mathematical Solution == | ||
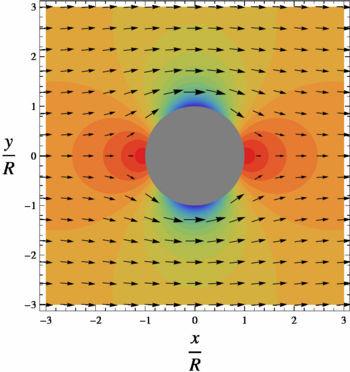
{{Image|Flow past a cylinder. Pressure field and velocity vectors.png|right|350px|Colors: pressure field. Red is high and blue is low. Velocity vectors.}} | {{Image|Flow past a cylinder. Pressure field and velocity vectors.png|right|350px|Colors: pressure field. Red is high and blue is low. Velocity vectors.}} | ||
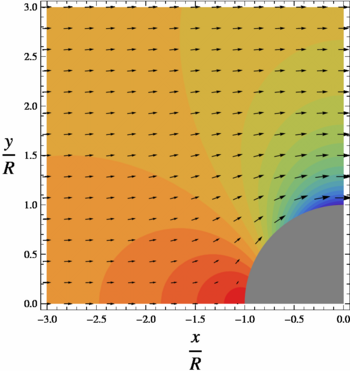
{{Image|Flow past a cylinder. Pressure field and velocity vectors. One quadrant.png|right|350px|Close-up view of one quadrant of the flow. Colors: pressure field. Red is high and blue is low. Velocity vectors.}} | |||
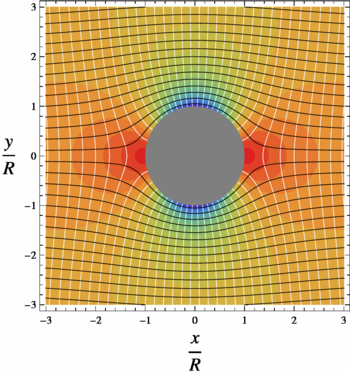
{{Image|Flow past a cylinder. Pressure streamfunction potential.png|right|350px|Pressure field (colors), streamfunction (black), velocity potential (white).}} | |||
A cylinder (or disk) of radius <math>R</math> is placed in two-dimensional, incompressible, inviscid flow. | A cylinder (or disk) of radius <math>R</math> is placed in two-dimensional, incompressible, inviscid flow. | ||
The goal is to find the velocity vector <math>\vec{V}</math> and pressure <math>p</math> in a plane, subject to the condition that | The goal is to find the steady velocity vector <math>\vec{V}</math> and pressure <math>p</math> in a plane, subject to the condition that | ||
far from the cylinder the velocity vector is | far from the cylinder the velocity vector is | ||
:<math>\vec{V}=U\widehat{i}+0\widehat{j}</math> | :<math>\vec{V}=U\widehat{i}+0\widehat{j}</math> | ||
and at the boundary of the cylinder | and at the boundary of the cylinder | ||
:<math>\vec{V}\cdot\widehat{n}=0</math> | :<math>\vec{V}\cdot\widehat{n}=0</math> | ||
where <math>\widehat{n}</math> is vector normal to the cylinder surface. | where <math>\widehat{n}</math> is vector normal to the cylinder surface. The upstream flow is uniform and has no vorticity. The flow is inviscid, incompressible and has constant mass density <math>\rho</math>. The flow therefore remains without vorticity, or is said to be ''irrotational'', with | ||
<math>\nabla \times \vec{V}=0</math> everywhere. Being irrotational, there must exist a velocity potential <math>\phi</math>: | |||
{ | :<math>\vec{V}=\nabla\phi</math> | ||
Being incompressible, <math>\nabla\cdot\vec{V}=0</math>, so <math>\phi</math> must satisify Laplace's equation: | |||
:<math> \nabla^2\phi=0</math> | |||
Revision as of 19:32, 29 May 2009
"The flow of an incompressible fluid past a cylinder is one of the first mathematical models that a student of fluid dynamics encounters. This flow is an excellent vehicle for the study of concepts that will be encountered numerous times in mathematical physics, such as vector fields, coordinate transformations, and most important, the physical interpretation of mathematical results." [1]
Mathematical Solution
A cylinder (or disk) of radius is placed in two-dimensional, incompressible, inviscid flow. The goal is to find the steady velocity vector and pressure in a plane, subject to the condition that far from the cylinder the velocity vector is
and at the boundary of the cylinder
where is vector normal to the cylinder surface. The upstream flow is uniform and has no vorticity. The flow is inviscid, incompressible and has constant mass density . The flow therefore remains without vorticity, or is said to be irrotational, with everywhere. Being irrotational, there must exist a velocity potential :
Being incompressible, , so must satisify Laplace's equation: