User talk:Paul Wormer/scratchbook1

Point-normal representation

PD Image
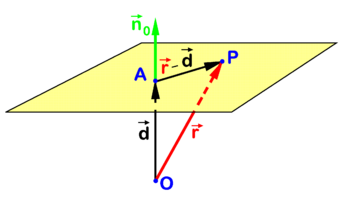
Fig. 1. Equation for plane. P is arbitary point in plane; Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle\vec{d}} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \scriptstyle \vec{n}_0 } are collinear.

In analytic geometry several closely related algebraic equations are known for a plane in three-dimensional Euclidean space. One such equation is illustrated in figure 1. Point P is an arbitrary point in the plane and O (the origin) is outside the plane. The point A in the plane is chosen such that vector

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{d} \equiv \overrightarrow{OA} }

is orthogonal to the plane. The collinear vector

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{n}_0 \equiv \frac{1}{d} \vec{d} \quad \hbox{with}\quad d \equiv \left|\vec{d}\,\right| }

is a unit (length 1) vector normal (perpendicular) to the plane which is known as the normal of the plane in point A. Note that d is the distance of O to the plane. The following relation holds for an arbitrary point P in the plane

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \left(\vec{r}-\vec{d}\;\right)\cdot \vec{n}_0 = 0 \quad\hbox{with}\quad \vec{r} \equiv\overrightarrow{OP}\quad\hbox{and}\quad \vec{r}-\vec{d} = \overrightarrow{AP} . }

This equation for the plane can be rewritten in terms of coordinates with respect to a Cartesian frame with origin in O. Dropping arrows for component vectors (real triplets) that are written bold, we find

$\left(\mathbf {r} -\mathbf {d} \right)\cdot \mathbf {n} _{0}=0\Longleftrightarrow xa_{0}+yb_{0}+zc_{0}=d$

with

$\mathbf {d} =(a,\;b,\;c),\quad \mathbf {n} _{0}=(a_{0},\;b_{0},\;c_{0}),\quad \mathbf {r} =(x,\;y,\;z),$

and

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{d}\cdot \mathbf{n}_0 = \frac{1}{d} \mathbf{d}\cdot \mathbf{d} = d = \sqrt{a^2+b^2+c^2}. }

Conversely, given the following equation for a plane

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle ax+by+cz = e, \, }

it is easy to derive the same equation. Write

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{r} = (x,\;y,\; z), \quad\mathbf{f} = (a,\;b,\; c), \quad\hbox{and}\quad \mathbf{d} \equiv \left(\frac{e}{a^2+b^2+c^2}\right) \mathbf{f}. }

It follows that

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{f}\cdot\mathbf{r} = e = \mathbf{f}\cdot \mathbf{d}. }

Hence we find the same equation,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{f}\cdot(\mathbf{r}-\mathbf{d}) = 0 \;\Longrightarrow\; (\mathbf{r}-\mathbf{d})\cdot\mathbf{n}_0 = 0 \quad\hbox{with}\quad \mathbf{n}_0 = \frac{1}{\sqrt{a^2+b^2+c^2}}\mathbf{f} }

where f , d, and n₀ are collinear. The equation may also be written in the following mnemonically convenient form

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mathbf{d}\cdot(\mathbf{r}-\mathbf{d}) = 0, }

which is the equation for a plane through a point A perpendicular to Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overrightarrow{OA}} .

Three-point representation

PD Image
Fig. 2. Plane through points A, B, and C.

Figure 2 shows a plane that by definition passes through non-coinciding points A, B, and C that moreover are not on one line. The point P is an arbitrary point in the plane and the reference point O is outside the plane. Referring to figure 2 we introduce the following definitions

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{a} = \overrightarrow{OA},\quad \vec{b} = \overrightarrow{OB},\quad\vec{c} = \overrightarrow{OC},\quad \vec{r} = \overrightarrow{OP}. }

Clearly the following two non-collinear vectors belong to the plane

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{u} = \overrightarrow{AB}= \vec{b}-\vec{a} ,\quad \vec{v} = \overrightarrow{AC}= \vec{c}-\vec{a}. }

Because a plane (an affine space), with a given fixed point as origin is a 2-dimensional linear space and two non-collinear vectors with "tails" in the origin are linearly independent, it follows that any vector in the plane can be written as a linear combination of these two non-collinear vectors (this is also expressed as: any vector in the plane can be decomposed into components along the two non-collinear vectors). In particular, taking A as origin in the plane,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overrightarrow{AP}= \vec{r}-\vec{a} = \lambda \vec{u} + \mu\vec{v},\qquad \lambda,\mu \in \mathbb{R}. }

The real numbers λ and μ specify the direction of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \overrightarrow{AP}} . Hence the following equation for the position vector Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{r}} of the arbitrary point P in the plane:

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{r} = \vec{a} + \lambda \vec{u} + \mu\vec{v} }

is known as the point-direction representation of the plane. This representation is equal to the three-point representation

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{r} = \vec{a}+ \lambda (\vec{b}-\vec{a}) + \mu(\vec{c}-\vec{a}), }

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{a}} , Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{b}} , and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{c}} are the position vectors of the three points that define the plane.

Writing for the position vector of the arbitrary point P in the plane

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{r} = (1-\lambda-\mu)\, \vec{a}+ \lambda\, \vec{b} + \mu\,\vec{c} \;\equiv\; \xi_1\, \vec{a} +\xi_2\,\vec{b} + \xi_3\, \vec{c}\; , }

we find that the real triplet (ξ₁, ξ₂, ξ₃) with ξ₁ + ξ₁ + ξ₁ = 1 forms a set of coordinates for P. The numbers {ξ₁, ξ₂, ξ₃ | ξ₁+ ξ₂+ ξ₃ = 1 } are known as the barycentric coordinates of P. It is trivial to go from barycentric coordinates to the "three-point representation",

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \vec{r} = \xi_1 \vec{a} + \xi_2\vec{b} + \xi_3 \vec{c}\quad\hbox{with}\quad \xi_1 = 1- \xi_2-\xi_3 \;\Longleftrightarrow\; \vec{r} = \vec{a} + \xi_2 (\vec{b}-\vec{a}) + \xi_3(\vec{c}-\vec{a}). }