imported>Paul Wormer |
imported>Paul Wormer |
| Line 1: |
Line 1: |
| Given are two unnormalized, non-parallel vectors, the rotation axis '''n''' and the vector '''r''' to be rotated.
| | {{Image|Pressure on pilbox.png|right|250px|A pillbox of height Δz and cross section ''O'' filled with air. Pillbox, with upward pressure ''p'' at its bottom, is part of a cylinder filled with air. Total mass ''M'' of air in pillbox is pulled downward by gravitational acceleration ''g'. }} |
| Decompose '''r''' into two orthogonal components:
| |
| :<math>
| |
| \mathbf{r} = \mathbf{n} \frac{\mathbf{n}\cdot\mathbf{r}}{n^2} + \underbrace{(\mathbf{r} -\mathbf{n} | |
| \frac{\mathbf{n}\cdot\mathbf{r}}{n^2} )}_{ \equiv\; \mathbf{x}} \quad\hbox{with}\quad n^2 \equiv\; \mathbf{n}\cdot\mathbf{n}
| |
| </math>
| |
| Clearly, '''n''' and '''x''' are orthogonal. Define further '''y''' as a [[cross product]], a vector orthogonal to the plane containing '''n''', '''r''', and '''x''',
| |
| :<math>
| |
| \mathbf{y} = \mathbf{n}\times \mathbf{r}.
| |
| </math>
| |
| As is shown [[vector product#Cross product as linear map|here]] the cross product can be written as a matrix-vector product
| |
| :<math>
| |
| \mathbf{y} = \mathbf{n}\times \mathbf{r}
| |
| = \begin{pmatrix} n_y r_z - n_z r_y \\ n_z r_x - n_x r_z \\ n_x r_y - n_y r_x \end{pmatrix}
| |
| = \underbrace{
| |
| \begin{pmatrix}
| |
| 0 & -n_z & n_y \\ | |
| n_z& 0 & -n_x \\
| |
| -n_y& n_x & 0
| |
| \end{pmatrix}}_{\mathbf{N}} \begin{pmatrix} r_x \\ r_y \\ r_z \end{pmatrix}
| |
| </math>
| |
| The matrix '''N''' has as general element
| |
| :<math>
| |
| N_{\alpha \beta} = - \epsilon_{\alpha \beta \gamma} n_\gamma \,
| |
| </math>
| |
| where ε<sub>αβγ</sub> is the antisymmetric [[Levi-Civita]] tensor.
| |
|
| |
|
| For further use we compute normalization constants of '''x''' and '''y''',
| | In the figure we see a stationary pillbox at arbitrary position ''z'' in a cylinder filled with air. The pillbox is pushed up by a [[pressure]] force ''pO'', and pulled down by gravitation, which gives a force '''G''' equal to the total mass ''M'' of air in the pillbox times the [[gravitational acceleration]] ''g''. Also the air pressure (''p''+ Δ''p'')''O'' at the top acts downward. Forces upward are positive, downward negative, and since the total force is zero (no motion of air), we have |
| :<math> | | :<math> |
| x^2 = \mathbf{x}\cdot \mathbf{x} = \left(\mathbf{r} -\mathbf{n} \frac{\mathbf{n}\cdot\mathbf{r}}{n^2} \right) \cdot
| | pO -Mg - (p+\Delta p)O = 0 \;\Longrightarrow \; \Delta p = - \frac{Mg}{O} |
| \left(\mathbf{r} -\mathbf{n} \frac{\mathbf{n}\cdot\mathbf{r}}{n^2}\right ) = r^2 - \frac{(\mathbf{n}\cdot\mathbf{r})^2}{n^2}
| |
| </math> | | </math> |
| | The total mass in the pillbox is the molar density ρ times the molar mass ''m'' times the volume of the pillbox Δ''z''·''O'' |
| :<math> | | :<math> |
| y^2 = (\mathbf{n}\times \mathbf{r})\cdot(\mathbf{n}\times \mathbf{r}) = n^2\,r^2 - (\mathbf{n}\cdot\mathbf{r})^2,
| | M = \rho m \Delta z O .\; |
| </math> | | </math> |
| and divide the two
| | Hence |
| :<math> | | :<math> |
| \frac{x^2}{y^2} = \frac{r^2 - \frac{(\mathbf{n}\cdot\mathbf{r})^2}{n^2}}{n^2\,r^2 - (\mathbf{n}\cdot\mathbf{r})^2} = \frac{1}{n^2}. | | \Delta p = - \rho m g \Delta z \, |
| </math> | | </math> |
| When we rotate '''r''' over an angle φ around '''n''', the component of '''r''' along '''n''' is unchanged, while the component '''x''' of '''r''' perpendicular to '''n''' becomes '''x'''′
| | Noting that the molar density is the number of moles per volume, we get for an [[ideal gas law|ideal gas]], |
| :<math> | | :<math> |
| \mathbf{x}' = \cos\phi\; \mathbf{x} + \frac{x}{y} \sin\phi \;\mathbf{y} = \cos\phi \;\mathbf{x} + \frac{1}{n} \sin\phi \;\mathbf{y}
| | p = \rho R T \;\Longrightarrow\; \rho = \frac{p}{RT} |
| </math> | | </math> |
| Hence the rotated vector '''r'''′ is
| | Assuming that the gas in the pillbox is ideal and of absolute [[temperature]] ''T'', we get |
| | the equation |
| :<math> | | :<math> |
| \mathbf{r}' = \mathbf{n} \frac{\mathbf{n}\cdot\mathbf{r}}{n^2} + | | \Delta p = - p \frac{mg}{RT} \Delta z \;\Longrightarrow\; |
| \cos\phi(\mathbf{r} -\mathbf{n} \frac{\mathbf{n}\cdot\mathbf{r}}{n^2} ) | | \frac{1}{p} \frac{\Delta p}{\Delta z} = - p \frac{mg}{RT} |
| +\frac{1}{n} \sin\phi \;\mathbf{N}\; \mathbf{r}
| | </math> |
| </math> | | Taking the limit of infinitesimal small Δ we obtain the differential equation |
| We may introduce the [[dyadic product]] of the vector '''n''' with itself, which has the form of a 3 × 3 symmetric matrix, and write
| |
| :<math> | | :<math> |
| \mathbf{n} \frac{\mathbf{n}\cdot\mathbf{r}}{n^2} =
| | \frac{d\ln\,p}{dz} = - \frac{mg}{RT} \qquad\qquad\qquad\qquad\qquad\qquad\qquad(1) |
| \frac{1}{n^2} \; \big(\mathbf{n}\otimes\mathbf{n}\big) \; \mathbf{r} \quad\hbox{with}\quad | |
| \big(\mathbf{n}\otimes\mathbf{n}\big)_{\alpha \beta} \equiv n_\alpha\; n_\beta.
| |
| </math> | | </math> |
| Now,
| | where we recall that the derivative of the natural logarithm is given by |
| :<math> | | :<math> |
| \mathbf{r}' = \left[ \cos\phi\; \mathbf{E} + \frac{(1-\cos\phi)}{n^2} \; \big(\mathbf{n}\otimes\mathbf{n}\big) | | \frac{d\ln f(x)}{dx} = \frac{1}{f(x)} \frac{df(x)}{dx}. |
| + \frac{1}{n} \sin\phi \;\mathbf{N} \right] \mathbf{r} ,
| |
| </math> | | </math> |
| where '''E''' is the identity matrix. The quantity between square brackets is the matrix '''R''' that rotates '''r''' around '''n''' over an angle φ. This equation is very well-known and was first derived by Leonhard Euler [check].
| | The master equation (1) can be solved by integrating the left hand side from ''p''<sub>0</sub> to |
| A general element of '''R''' is
| | ''p'' and the right hand side from ''z''<sub>0</sub> to ''z''. Hence |
| :<math> | | :<math> |
| R_{\alpha \beta} = \cos\phi\; \delta_{\alpha \beta} + \frac{(1-\cos\phi)}{n^2} n_\alpha n_\beta - \frac{\sin\phi}{n} \epsilon_{\alpha \beta\gamma} n_\gamma =
| | \ln\frac{p}{p_0} = - \frac{mg}{RT} (z-z_0) \qquad\qquad\qquad\qquad\qquad(2) |
| \cos\phi\; \delta_{\alpha \beta} + (1-\cos\phi)\hat{n}_\alpha \hat{n}_\beta - \sin\phi\; \epsilon_{\alpha \beta\gamma}\; \hat{n}_\gamma,
| |
| </math> | | </math> |
| where the unit vector is | | where we recall that |
| :<math> | | :<math> |
| \hat\mathbf{n} \equiv \frac{\mathbf{n}}{n}. | | \ln p - \ln p_0 = \ln\frac{p}{p_0} |
| </math> | | </math> |
| Möller and Hughes (1999) refer to this century-old equation for the elements of '''R''' as the "Foley (1990) equation".
| | Taking the exponent (the inverse function of the natural logarithm) of both sides of equation (2) |
| For normalized '''n''' the rotated vector may be written as:
| | we get |
| :<math> | | :<math> |
| r'_{\alpha} = \sum_\beta R_{\alpha \beta} r_\beta =
| | \frac{p}{p_0} = \frac{\exp\left[- \frac{mg}{RT} z\right]}{\exp\left[- \frac{mg}{RT} z_0\right]} |
| \sum_\beta \left[\cos\phi\; \delta_{\alpha \beta} + (1-\cos\phi)\hat{n}_\alpha \hat{n}_\beta - \sin\phi\; \epsilon_{\alpha \beta\gamma}\; \hat{n}_\gamma\right] r_\beta \quad \Rightarrow\quad | | \;\Longleftrightarrow\; |
| \mathbf{r}' = \mathbf{r}\;\cos\phi + \hat{\mathbf{n}}\;\big(\hat{\mathbf{n}}\cdot \mathbf{r}\big)\big(1-\cos\phi\big)
| | p = p_0 \, \exp\left[ - \frac{mg}{RT}(z-z_0) \right] |
| + (\hat{\mathbf{n}}\times\mathbf{r} )\;\sin\phi.
| |
| </math> | | </math> |
| Consider now two non-parallel unit vectors '''f''' and '''t''' making an angle φ
| | This is distribution is know in [[statistical thermodynamics]] as a [[Boltzmann distribution]]. |
| | |
| | We assumed here that ''T'' is constant throughout the cylinder, which makes the equation useful for cases where there is no temperature gradient, i.e., case where the temperature at the top of the cylinder is equal to the temperature at the bottom. The master equation (1) can be modified for the case of a constant temperature gradient (constant [[lapse rate]]). That is, we make the substitution |
| :<math> | | :<math> |
| \mathbf{f} \cdot \mathbf{t} = \cos\phi \quad \hbox{and}\quad |\mathbf{f} \times \mathbf{t}| = \sin\phi
| | T \rightarrow T + K (z-z_0) |
| </math>
| | </math> |
| We want to find the matrix that rotates '''f''' (the "from" vector) to '''t''' (the "to" vector). An obvious way is using the cross product '''f'''×'''t''' as a rotation axis and rotating '''f''' over φ. We can use the equation just derived by substituting
| | in equation (1). The modified equation is still easily integrated. |
| :<math>
| |
| \mathbf{n} \rightarrow \mathbf{f} \times \mathbf{t} \quad\hbox{and}\quad n \rightarrow \sin\phi.
| |
| </math>
| |
| Hence
| |
| :<math>
| |
| \frac{(1-\cos\phi)}{n^2} = \frac{(1-\cos\phi)}{1-\cos^2\phi} = \frac{1}{1+\cos\phi}
| |
| </math> | |
| so that an element of the rotation matrix takes the form
| |
| :<math>
| |
| R_{\alpha \beta} = \cos\phi\; \delta_{\alpha \beta} + \frac{1}{1+\cos\phi} n_\alpha n_\beta - \epsilon_{\alpha \beta\gamma} n_\gamma,
| |
| </math>
| |
| which is Eq. (1) of Möller and Hughes (1999) modified by dividing out (1 - cosφ) in the second term, which M and H don't do.
| |
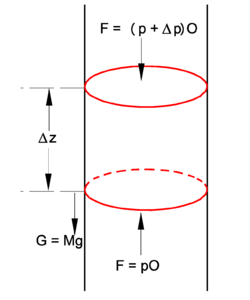
PD Image A pillbox of height Δz and cross section
O filled with air. Pillbox, with upward pressure
p at its bottom, is part of a cylinder filled with air. Total mass
M of air in pillbox is pulled downward by gravitational acceleration
g'. In the figure we see a stationary pillbox at arbitrary position z in a cylinder filled with air. The pillbox is pushed up by a pressure force pO, and pulled down by gravitation, which gives a force G equal to the total mass M of air in the pillbox times the gravitational acceleration g. Also the air pressure (p+ Δp)O at the top acts downward. Forces upward are positive, downward negative, and since the total force is zero (no motion of air), we have
The total mass in the pillbox is the molar density ρ times the molar mass m times the volume of the pillbox Δz·O
Hence
Noting that the molar density is the number of moles per volume, we get for an ideal gas,
Assuming that the gas in the pillbox is ideal and of absolute temperature T, we get
the equation
Taking the limit of infinitesimal small Δ we obtain the differential equation
where we recall that the derivative of the natural logarithm is given by
The master equation (1) can be solved by integrating the left hand side from p0 to
p and the right hand side from z0 to z. Hence
where we recall that
Taking the exponent (the inverse function of the natural logarithm) of both sides of equation (2)
we get
![{\displaystyle {\frac {p}{p_{0}}}={\frac {\exp \left[-{\frac {mg}{RT}}z\right]}{\exp \left[-{\frac {mg}{RT}}z_{0}\right]}}\;\Longleftrightarrow \;p=p_{0}\,\exp \left[-{\frac {mg}{RT}}(z-z_{0})\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/218b3157c56c311be32e3c191ebe8f04e95bca1b)
This is distribution is know in statistical thermodynamics as a Boltzmann distribution.
We assumed here that T is constant throughout the cylinder, which makes the equation useful for cases where there is no temperature gradient, i.e., case where the temperature at the top of the cylinder is equal to the temperature at the bottom. The master equation (1) can be modified for the case of a constant temperature gradient (constant lapse rate). That is, we make the substitution
in equation (1). The modified equation is still easily integrated.
