User:Milton Beychok/Sandbox

(PD) Diagram: Milton Beychok
Diagram of the gas flow through a de Laval nozzle used to produce supersonic velocity of the exhaust gases from a rocket engine.

A de Laval nozzle (also convergent-divergent nozzle) is a tube that is pinched in the middle, making a carefully balanced, asymmetric hourglass-shape. It is used to accelerate a hot, pressurized gas passing through it to a supersonic speed, and upon expansion, to shape the exhaust flow so that the heat energy propelling the flow is maximally converted into directed kinetic energy.

The de Lava nozzle is widely used in some types of steam turbine and it is an essential part of modern rocket engines as well as being used in supersonic jet engines.

Similar flow properties have been ascribed to jet streams within astrophysics.

History

The nozzle was developed by Swedish inventor Gustaf de Laval in 1888 for use on an impulse steam turbine.

A de Laval nozzle was used in the first liquid fuel rocket engine designed and launched in 1926 by Robert Goddard, an American physicist and rocket pioneer. It is now used in nearly all modern rocket engines propelled by the hot gases produced by combustion of a fuel.

Operation

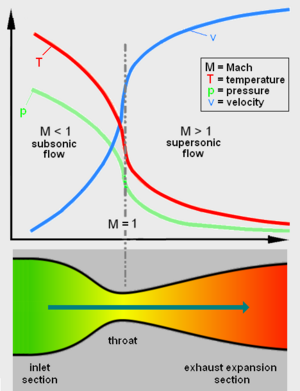
Its operation relies on the different properties of gases flowing at subsonic and supersonic speeds. The speed of a subsonic flow of gas will increase if the pipe carrying it narrows because the mass flow rate is constant. The gas flow through a de Laval nozzle is isentropic (gas entropy is nearly constant). At subsonic flow the gas is compressible; sound, a small pressure wave, will propagate through it. At the "throat", where the cross sectional area is a minimum, the gas velocity locally becomes sonic (Mach number = 1.0), a condition called choked flow. As the nozzle cross sectional area increases the gas begins to expand and the gas flow increases to supersonic velocities where a sound wave will not propagate backwards through the gas as viewed in the frame of reference of the nozzle (Mach number > 1.0).

Conditions for operation

A de Laval nozzle will only choke at the throat if the pressure and mass flow through the nozzle is sufficient to reach sonic speeds, otherwise no supersonic flow is achieved and it will act as a Venturi tube.

In addition, the pressure of the gas at the exit of the expansion portion of the exhaust of a nozzle must not be too low. Because pressure cannot travel upstream through the supersonic flow, the exit pressure can be significantly below ambient pressure it exhausts into, but if it is too far below ambient, then the flow will cease to be supersonic, or the flow will separate within the expansion portion of the nozzle, forming an unstable jet that may 'flop' around within the nozzle, possibly damaging it.

In practice ambient pressure must be no higher than roughly 2-3 times the pressure in the supersonic gas at the exit for supersonic flow to leave the nozzle.

Analysis of gas flow in de Laval nozzles

The analysis of gas flow through de Laval nozzles involves a number of concepts and assumptions:

• For simplicity, the gas is assumed to be an ideal gas.
• The gas flow is isentropic (i.e., at constant entropy). As a result the flow is reversible (frictionless and no dissipative losses), and adiabatic (i.e., there is no heat gained or lost).
• The gas flow is constant (i.e., steady) during the period of the propellant burn.
• The gas flow is along a straight line from gas inlet to exhaust gas exit (i.e., along the nozzle's axis of symmetry)
• The gas flow behavior is compressible since the flow is at very high velocities.

Exhaust gas velocity

As the gas enters a nozzle, it is traveling at subsonic velocities. As the throat contracts down the gas is forced to accelerate until at the nozzle throat, where the cross-sectional area is the smallest, the linear velocity becomes sonic. From the throat the cross-sectional area then increases, the gas expands and the linear velocity becomes progressively more supersonic.

The linear velocity of the exiting exhaust gases can be calculated using the following equation:

$V_{e}={\sqrt {\;{\frac {T\;R}{M}}\cdot {\frac {2\;k}{k-1}}\cdot {\bigg [}1-(P_{e}/P)^{(k-1)/k}{\bigg ]}}}$

where:
Ve	= Exhaust velocity at nozzle exit, m/s
T	= absolute temperature of inlet gas, K
R	= Universal gas law constant = 8314.5 J/(kmol·K)
M	= the gas molecular mass, kg/kmol    (also known as the molecular weight)
k	= cp/cv = isentropic expansion factor
cp	= specific heat of the gas at constant pressure
cv	= specific heat of the gas at constant volume
Pe	= absolute pressure of exhaust gas at nozzle exit, Pa
P	= absolute pressure of inlet gas, Pa

Some typical values of the exhaust gas velocity V_e for rocket engines burning various propellants are:

• 1700 to 2900 m/s (3,800 to 6,500 mph) for liquid monopropellants
• 2900 to 4500 m/s (6,500 to 10,100 mph) for liquid bipropellants
• 2100 to 3200 m/s (4,700 to 7,200 mph) for solid propellants

As a note of interest, V_e is sometimes referred to as the ideal exhaust gas velocity because it based on the assumption that the exhaust gas behaves as an ideal gas.

As an example calculation using the above equation, assume that the propellant combustion gases are: at an absolute pressure entering the nozzle of P = 7.0 MPa and exit the rocket exhaust at an absolute pressure of P_e = 0.1 MPa; at an absolute temperature of T = 3500 K; with an isentropic expansion factor of k = 1.22 and a molar mass of M = 22 kg/kmol. Using those values in the above equation yields an exhaust velocity V_e = 2802 m/s or 2.80 km/s which is consistent with above typical values.

The technical literature can be very confusing because many authors fail to explain whether they are using the universal gas law constant R which applies to any ideal gas or whether they are using the gas law constant R_s which only applies to a specific individual gas. The relationship between the two constants is R_s = R/M.

Examples

For example a de Laval nozzle using hot air at a pressure of 1,000 psi (6.9 MPa or 68 atm), temperature of 1470 K, would have a pressure of 540 psi (3.7 MPa or 37 atm), temperature of 1269 K at the throat, and 15 psi (0.1 MPa or 1 atm), temperature of 502 K at the nozzle exit. The expansion ratio, nozzle cross sectional area at exit divided by area at throat, would be 6.8. The specific impulse would be 151 s (1480 N·s/kg).

Application to celestial objects

Theoretical astrophysicists have found that pipes with the flow pattern of a De Laval nozzle have analogous phenomena in the interstellar medium. The interior of an accretion disk has a similar function as the pipe, save it is not a solid wall, but itself a fluid that can contain a relativistic jet by a pressure balanced boundary.

References

Bibliography:

• Garrett Scaife (2000). From Galaxies to Turbines: Science, Technology, and the Parsons Family. Taylor & Francis Group, page 197. ISBN 0-7503-0582-7.  Available on-line at Google books

• John David Anderson (2003). Modern Compressible Flow: With Historical Perspective, 3rd Edition. McGraw-Hill, page 229. ISBN 0-07-242443-5.  Available on-line at Google books