Newton's method: Difference between revisions
imported>Fredrik Johansson |
imported>Fredrik Johansson |
||
| Line 58: | Line 58: | ||
It may also happen that Newton's method converges to a root, but the wrong one. For example, if we attempt to calculate <math>\pi</math> as the smallest positive solution to <math>\sin x = 0</math>, we must choose an initial value close to 3.14. Newton's method started near 0 would converge to 0; if started near 6.28, it would converge to <math>2\pi</math>. If we start with <math>x_0</math> close to <math>\pi/2</math>, where the sine curve is horizontal, <math>x_1</math> may end up close to <math>n \pi</math> for some enormous ''n''. | It may also happen that Newton's method converges to a root, but the wrong one. For example, if we attempt to calculate <math>\pi</math> as the smallest positive solution to <math>\sin x = 0</math>, we must choose an initial value close to 3.14. Newton's method started near 0 would converge to 0; if started near 6.28, it would converge to <math>2\pi</math>. If we start with <math>x_0</math> close to <math>\pi/2</math>, where the sine curve is horizontal, <math>x_1</math> may end up close to <math>n \pi</math> for some enormous ''n''. | ||
<center> | |||
{| | |||
|[[Image:Newton's method cycle.png|thumb|center|250px|Newton's method stuck in a cycle on the problem <math>x^3 - 5x = 0</math>.]] | |||
|[[Image:Newton's method sine.png|thumb|center|250px|Outcome of Newton's method applied to finding a root of the sine function. Initial values near 0 (blue) lead to 0 while initial values near <math>\pi</math> (green) lead to <math>\pi</math>. Values close to <math>\pi/2</math> may lead anywhere on the real line; the initial value <math>x_0 = 1.475</math> (red) depicted here leads to <math>-3\pi</math>.]] | |||
|} | |||
</center> | |||
===Complex functions=== | ===Complex functions=== | ||
Revision as of 02:16, 11 April 2007
Newton's method, also called the Newton-Raphson method or Newton iteration, is a root-finding algorithm; that is, a method for finding where a function obtains the value zero.
Description of the method
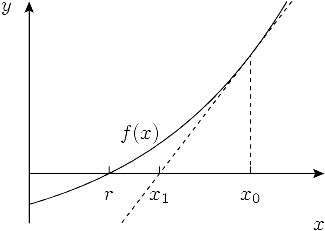
Newton's method is based on the insight that any smooth function f can be approximated locally by its tangent. If r is a root of f, the tangent of f at any point close to r is a good approximation of f, and hence the point where the tangent intercepts the x-axis is a good approximation of r. This suggests that if we know an approximation xk for r, we obtain an even better approximation xk+1 from the root of the tangent line that goes through (x, f(x)). Expressing the equation for the tangent in the terms of , the derivative of f, gives the solution
The calculation of an improved approximation with this formula is called a Newton step or Newton update. Newton's method consists of repeating this step for k = 0, 1, 2, ... to obtain successively better estimates x1, x2, x3, ... for r. Provided that the initial guess x0 is sufficiently close to r and that f is sufficiently well-behaved, the estimates will converge rapidly to r as k goes to infinity.
Example: calculating the golden ratio
The golden ratio (φ ≈ 1.618) is the largest root of the polynomial . To calculate this root, we can use the Newton iteration
with the initial estimate x0 = 1. Using double-precision floating-point arithmetic, which allows a precision of roughly 16 digits, Newton's method produces the following sequence of approximations:
- x0 = 1.0
- x1 = 2.0
- x2 = 1.6666666666666667
- x3 = 1.6190476190476191
- x4 = 1.6180344478216817
- x5 = 1.618033988749989
- x6 = 1.6180339887498947
- x7 = 1.6180339887498949
- x8 = 1.6180339887498949
Since the last update does not change the value, we can be reasonably sure to have obtained a value for the golden ratio that is correct to the available precision. It can be seen that each iteration roughly doubles the number of correct digits. We say that the rate of convergence is quadratic. Newton's method typically — but not always — achieves such fast convergence.
Convergence analysis
Intuitively, Newton's method is based on the idea that a continuous function f can be approximated locally by a line. If both the root r and the initial guess lie in a region where f is "sufficiently linear" — we may call such an area a region of convergence, Newton's method is guaranteed to converge to the root.
The convergence rate of Newton's method can be derived using Taylor series. Taking the Taylor series of f around xk gives
where . Assuming , dividing through gives
Moving terms to the left hand side and substituting the Newton update expression for xk+1 then gives
and a final division shows that
This is the expression for a rate of convergence that is at least quadratic. If the second derivative vanishes near the root, the convergence is faster than quadratic. However, if , meaning that f has a double root, the result becomes slightly different: it can then be shown that the convergence is only linear.
Most functions do not globally resemble lines: in general, function graphs contain curvature, stationary points, and discontinuities. Does Newton's method work in these cases? The answer is maybe. If we start with an initial guess that lies outside a region of convergence, Newton's method produces a sequence of numbers that may jump back and forth erratically or even gradually move away from the root. If we are lucky, a value eventually ends up a region of convergence. But if we are unlucky, Newton's method may entirely fail to converge.
For example, if Newton's method is used to solve the equation with the initial guess , it will produce the endlessly repeating sequence .
It may also happen that Newton's method converges to a root, but the wrong one. For example, if we attempt to calculate as the smallest positive solution to , we must choose an initial value close to 3.14. Newton's method started near 0 would converge to 0; if started near 6.28, it would converge to . If we start with close to , where the sine curve is horizontal, may end up close to for some enormous n.
Complex functions
Newton's method also works for complex functions, but its convergence behavior become more intricate.
Leads to Newton fractals.
Newton's method as an optimization algorithm
Instead iterate
Multidimensional version
Gauss-Newton's method
Variations and practical implementation concerns
Damped, bracketed and hybrid methods
The fact that Newton's method may converge slowly or fail to converge for functions with horizontal tangents, or when given poor initial values, makes it unsuitable in raw form as a general-purpose root-finding algorithm. It is therefore typically combined with some mechanism for detecting and correcting convergence failure.
One way to detect failure is count the number of iterations and break if the number exceeds some specified limit. Another technique is bracketing: the root is supplied along with known bounds for its location. Failure is signaled if the Newton iteration produces a value that lies outside the bounds.
In case of failure, it may be possible to recover by switching to a slower but safer algorithm, such as the bisection algorithm. After taking a few steps with the safe method, one can switch back to Newton's method and try again. This is called a hybrid method. Another option is the damped Newton's method, in which the derivative is multiplied by a damping factor , with .
Quasi-Newton methods
Newton's method requires that the derivative of the object function be known, but in some situations the derivative or Jacobian may be unavailable or prohibitively expensive to calculate. The cost can be higher still when Newton's method is used as an optimization algorithm, in which case the second derivative or Hessian is also needed.
An alternative in these situations is to use an approximation of the derivative or second-derivative, which leads to so-called quasi-Newton methods. The most common strategy is to use the function values from two successive iterations to calculate a finite difference approximation for the derivative. This is equivalent to the secant method and reduces the rate of convergence from 2 to 1.618 (more precisely, the golden ratio). An alternative is to compute a value for the derivative or second derivative accurately, but reusing the same value for several successive iterations.
Modifications of Newton's method can also lead to more specialized algorithms, such as the Durand-Kerner method which is used to find simultaneous roots of a polynomial.
Calculating inverse functions
Using Newton's method as described above, the time complexity of finding a simple root of a function f with n-digit precision is where F is the cost of calculating with n-digit precision. If f can be evaluated with variable precision, the algorithm can be improved. Because of the "self-correcting" nature of Newton's method, it is only necessary to use m-digit precision at a step where the approximation has m-digit accuracy. Hence, the first iteration can be performed with a precision twice as high as the accuracy of x0, the second iteration with a precision four times as high, and so on. If the precision levels are chosen suitably, only the final iteration requires f and its derivative to be evaluated at full n-digit precision. Provided that F grows superlinearly, which is the case in practice, the cost of finding a root is thus only .
Root-finding is essentially the same thing as calculating an inverse function. Hence, due to the aforementioned result, two differentiable functions that are inverse functions of each other have equivalent computational complexity and can be calculated in terms of each other in practice using Newton's method. In particular, it can be shown that:
- The exponential function, the natural logarithm, the trigonometric functions, and the inverse trigonometric functions, are all equivalent
- The algebraic operations of multiplication, division, and square root extraction are equivalent
During the second half of the 20th century, very efficient algorithms were found for multiplying large numbers and calculating high-precision natural logarithms with the aid of computers. Combined with Newton's method, all of the functions listed above can be calculated with this efficiency.
History
Newton's method was described by Isaac Newton in De analysi per aequationes numero terminorum infinitas (written in 1669, published in 1711 by William Jones) and in De metodis fluxionum et serierum infinitarum (written in 1671, translated and published as Method of Fluxions in 1736 by John Colson). However, his description differs substantially from the modern description given above: Newton applies the method only to polynomials. He does not compute the successive approximations xk, but computes a sequence of polynomials and only at the end, he arrives at an approximation for the root r. Finally, Newton views the method as purely algebraic and fails to notice the connection with calculus. Isaac Newton probably derived his method from a similar but less precise method by François Viète. The essence of Viète's method can be found in the work of Sharaf al-Din al-Tusi.
Newton's method was first published in 1685 in A Treatise of Algebra both Historical and Practical by John Wallis. In 1690, Joseph Raphson published a simplified description in Analysis aequationum universalis. Raphson again viewed Newton's method purely as an algebraic method and restricted its use to polynomials, but he describes the method in terms of the successive approximations xk instead of the more complicated sequence of polynomials used by Newton. Finally, in 1740, Thomas Simpson described Newton's method as an iterative methods for solving general nonlinear equations using fluxional calculus, essentially giving the description above. In the same publication, Simpson also gives the generalization to systems of two equations and notes that Newton's method can be used for solving optimization problems by setting the gradient to zero.
References
- Michael T. Heath (2002), Scientific Computing: An Introductory Survey, Second Edition, McGraw-Hill
- Jonathan M. Borwein & Peter B. Borwein (1987), Pi and the AGM: A Study in Analytic Number Theory and Computational Complexity, Wiley Interscience
- Tjalling J. Ypma (1995), Historical development of the Newton-Raphson method, SIAM Review 37 (4), 531–551.






![{\displaystyle \xi _{k}\in [r,x_{k}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d5b4541fd20e7a356be47b342c4adf48e89b4100)
























