Group (mathematics)/Catalogs: Difference between revisions
Jump to navigation
Jump to search

imported>Ragnar Schroder (cosmetics) |
imported>Ragnar Schroder (→Different classes of groups: cosmetics) |
||
| Line 14: | Line 14: | ||
===Examples of finite discrete groups=== | ===Examples of finite discrete groups=== | ||
{|align=" | # The trivial group consisting of just one element. | ||
|''' | # The group of order two, which f.i. can be represented by addition [[modular arithmetic|modulo]] 2 or the set {-1, 1} under multiplication. | ||
# The group of order three. | |||
# The [[cyclic group]] of order 4, which can be represented by addition [[modular arithmetic|modulo]] 4. | |||
# The noncyclic group of order 4, known as the "Klein [[viergruppe]]". A simple physical model of this group is two separate on-off switches. | |||
{|align="center" cellpadding="10" style="background-color:lightgray; width:75%; border: 1px solid #aaa; margin:2px; font-size: 90%;" | |||
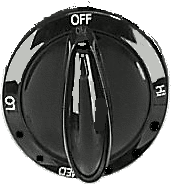
|'''Model of the [[cyclic group]] of order 4.''' | |||
[[Image:Examplesofgroups-Z4.gif|right|thumb|350px|{{#ifexist:Template:Examplesofgroups-Z4.gif/credit|{{Examplesofgroups-Z4.gif/credit}}<br/>|}} Example of groups.]] | [[Image:Examplesofgroups-Z4.gif|right|thumb|350px|{{#ifexist:Template:Examplesofgroups-Z4.gif/credit|{{Examplesofgroups-Z4.gif/credit}}<br/>|}} Example of groups.]] | ||
*Let | *Let r<sub>1</sub> be the act of turning the knob 1 step clockwise. | ||
*Let | *Let r<sub>2</sub> be the act of turning the knob 2 steps clockwise. | ||
*Let | *Let r<sub>3</sub> be the act of turning the know 3 steps clockwise. | ||
*Finally, let | *Finally, let r<sub>0</sub> be the act of just doing nothing. | ||
It's easy to see the following: | It's easy to see the following: | ||
*Doing | *Doing r<sub>1</sub> and then r<sub>1</sub> again gives the same result as doing r<sub>2</sub>. | ||
*Doing | *Doing r<sub>1</sub> and then r<sub>2</sub> gives the same result as doing r<sub>3</sub>. | ||
*Doing | *Doing r<sub>1</sub> and then r<sub>3</sub> gives the same result as doing nothing, i.e. r<sub>0</sub>. | ||
*... | *... | ||
| Line 33: | Line 39: | ||
These results can be summarized in the following table: | These results can be summarized in the following table: | ||
<table> | <table> | ||
<th>*</th> <th> | <th>*</th> <th>r<sub>0</sub></th> <th>r<sub>1</sub></th> <th>r<sub>2</sub></th> <th>r<sub>3</sub></th> | ||
<tr> | <tr> | ||
<td><b> | <td><b>r<sub>0</sub></b></td> <td>r<sub>0</sub></td> <td>r<sub>1</sub></td> <td>r<sub>2</sub></td> <td>r<sub>3</sub></td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td><b> | <td><b>r<sub>1</sub></b></td> <td>r<sub>1</sub></td> <td>r<sub>2</sub></td> <td>r<sub>3</sub></td> <td>r<sub>0</sub></td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td><b> | <td><b>r<sub>2</sub></b></td> <td>r<sub>2</sub></td> <td>r<sub>3</sub></td> <td>r<sub>0</sub></td> <td>r<sub>1</sub></td> | ||
</tr> | </tr> | ||
<tr> | <tr> | ||
<td><b> | <td><b>r<sub>3</sub></b></td> <td>r<sub>3</sub></td> <td>r<sub>0</sub></td> <td>r<sub>1</sub></td> <td>r<sub>2</sub></td> | ||
</tr> | </tr> | ||
</table> | </table> | ||
| Line 50: | Line 56: | ||
Many examples of groups come from considering some object and a set of bijective functions from the object to itself, which preserve some structure that this object has. | |||
Many | |||
* [[Topological groups]]: | * [[Topological groups]]: | ||
Revision as of 17:48, 28 November 2007
The mathematical group concept represents a rather simple and natural generalization of common phenomena, so examples of groups are easily found, from all areas of mathematics.
Different classes of groups
Three different classes of groups are commonly studied:
Examples of finite discrete groups
- The trivial group consisting of just one element.
- The group of order two, which f.i. can be represented by addition modulo 2 or the set {-1, 1} under multiplication.
- The group of order three.
- The cyclic group of order 4, which can be represented by addition modulo 4.
- The noncyclic group of order 4, known as the "Klein viergruppe". A simple physical model of this group is two separate on-off switches.
Model of the cyclic group of order 4.
It's easy to see the following:
|
Many examples of groups come from considering some object and a set of bijective functions from the object to itself, which preserve some structure that this object has.