User:John R. Brews/Sample2

(PD) Image: John R. Brews
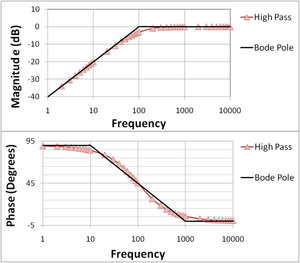
The Bode plot for a first-order (one-pole) highpass filter; the straight-line approximations are labeled "Bode pole"; phase varies from 90° at low frequencies (due to the contribution of the numerator, which is 90° at all frequencies) to 0° at high frequencies (where the phase contribution of the denominator is −90° and cancels the contribution of the numerator).

(PD) Image: John R. Brews
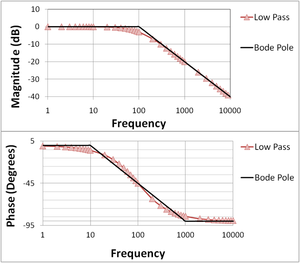
The Bode plot for a first-order (one-pole) lowpass filter; the straight-line approximations are labeled "Bode pole"; phase is 90° lower than for the highpass filter because the phase contribution of the numerator is 0° at all frequencies.

A Bode plot, named after Hendrik Wade Bode, is a combination of a Bode magnitude plot and Bode phase plot:

A Bode magnitude plot is a graph of log magnitude versus frequency, plotted with a log-frequency axis, to show the transfer function or frequency response of a linear, time-invariant system. The magnitude axis of the Bode plot is usually expressed as decibels, that is, 20 times the common logarithm of the amplitude of the gain.

A Bode phase plot is a graph of phase versus frequency, also plotted on a log-frequency axis,to evaluate how much a signal will be phase-shifted. The phase shift φ is generally a function of frequency.

The two Bode plots can be seen as separate plots of the real and the imaginary parts of the complex logarithm of a complex gain, say A(φ) = |A|e^jφ. The Bode plot of a gain that is the product of two gains, A = A₁A₂ is thus:

$\ln \left(|A_{1}|e^{j\varphi _{1}}\ \cdot \ |A_{2}|e^{j\varphi _{2}}\right)$ $=\ln \left(|A_{1}||A_{2}|\right)+\ln e^{j(\varphi _{1}+\varphi _{2})}$ $=\left(\log |A_{1}|+\ln |A_{2}|\right)+j(\varphi _{1}+\varphi _{2})\ .$

That is, once the natural logarithms of the gain magnitudes are converted to dB, the Bode plot of the product is expressed by the two Bode plots: the sum of the Bode magnitude plots and the sum of the Bode phase plots.

In the figure at right, the Bode magnitude and phase plots are shown for a one-pole highpass filter function:

$\mathrm {A_{High}} (f)={\frac {jf/f_{1}}{1+jf/f_{1}}}\ ,$

where f is the frequency in Hz, and f₁ is the pole position in Hz, f₁ = 100 Hz in the figure. Using the rules for complex numbers, the magnitude of this function is

$\mid \mathrm {A_{High}} (f)\mid ={\frac {f/f_{1}}{\sqrt {1+(f/f_{1})^{2}}}}\ ,$

while the phase is:

$\varphi _{A_{High}}=90^{\circ }-\mathrm {tan^{-1}} (f/f_{1})\ .$

The adjective highpass refers to the behavior that high frequency signals are transferred unchanged, while low frequency signals are attenuated.

Care must be taken that the inverse tangent is set up to return degrees, not radians. On the Bode magnitude plot, decibels are used, and the plotted magnitude is:

$20\ \mathrm {log_{10}} \mid \mathrm {A_{High}} (f)\mid \ =20\ \mathrm {log_{10}} \left(f/f_{1}\right)$

  $\ -20\ \mathrm {log_{10}} \left({\sqrt {1+(f/f_{1})^{2}}}\right)\ .$

In the next figure, the Bode plots are shown for the one-pole lowpass filter function:

$\mathrm {A_{Low}} (f)={\frac {1}{1+jf/f_{1}}}\ .$

The lowpass adjective describes the unattenuated passage of low-frequency signals and the attenuation of high-frequency signals.

Circuit modifications seldom change the magnitude and phase Bode plots independently — changing the amplitude response of the system will most likely change the phase characteristics and vice versa. Their interdependence is illustrated by the observation that the phase and amplitude characteristics can be obtained from each other for minimum-phase systems using the Hilbert transform.

If the transfer function is a rational function with real poles and zeros, then the Bode plot can be approximated with straight lines. These asymptotic approximations are called straight line Bode plots. Also shown in these two figures are these straight-line approximations to the Bode plots.

An example with pole and zero

(PD) Image: John R. Brews
Bode magnitude plot for zero and for low-pass pole; curves labeled "Bode" are the straight-line Bode plots.

(PD) Image: John R. Brews
Bode phase plot for zero and for low-pass pole; curves labeled "Bode" are the straight-line Bode plots.

(PD) Image: John R. Brews
Bode magnitude plot for pole-zero combination; the location of the zero is ten times higher than in above figures; curves labeled "Bode" are the straight-line Bode plots

(PD) Image: John R. Brews
Bode phase plot for pole-zero combination; the location of the zero is ten times higher than in above figures; curves labeled "Bode" are the straight-line Bode plots.

The construction of Bode plots using superposition now is illustrated. To begin, the components are presented separately.

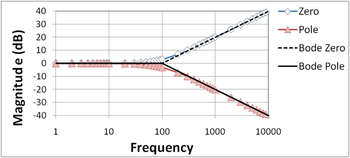
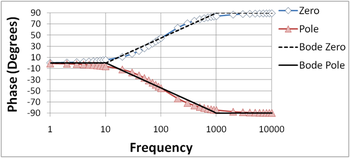
The figure at right shows the Bode magnitude plot for a zero and a low-pass pole, and compares the two with the Bode straight line plots. The straight-line plots are horizontal up to the pole (zero) location and then drop (rise) at 20 dB/decade. The figure below does the same for the phase. The phase plots are horizontal up to a frequency a factor of ten below the pole (zero) location and then drop (rise) at 45°/decade until the frequency is ten times higher than the pole (zero) location. The plots then are again horizontal at higher frequencies at a final, total phase change of 90°.

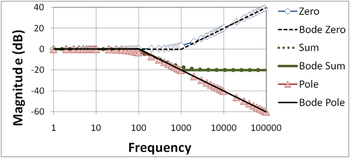
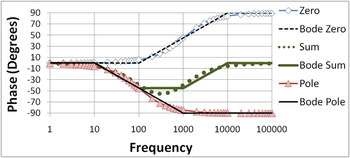
The Bode plot for a gain function that is the product of a pole and zero can be constructed by superposition, because the Bode plot is logarithmic, and the logarithm of a product of factors is sum of the individual, separate logarithms. The following two figures show how superposition (simple addition) of a pole and zero plot is done. The Bode straight line plots again are compared with the exact plots. The zero is assumed to reside at higher frequency than the pole to make a more interesting example.

Notice in the magnitude plot that the initial 20 dB/decade drop of the pole is arrested by the onset of the 20 dB/decade rise of the zero, resulting in a horizontal (zero-slope) magnitude plot for frequencies above the zero location.

Notice in the bottom phase plot that the straight-line approximation is very approximate in the region where both pole and zero affect the phase. Notice also in this plot that the range of frequencies where the phase changes in the straight line plot is limited to frequencies a factor of ten above and below the pole (zero) location. Where the phase of the pole and the zero both are present, the straight-line phase plot is horizontal because the 45°/decade drop of the pole is arrested by the overlapping 45°/decade rise of the zero in the limited range of frequencies where both are active contributors to the phase.

Gain margin and phase margin

Bode plots are used to assess the stability of negative feedback amplifiers by finding the gain and phase margins of an amplifier. The notion of gain and phase margin is based upon the gain expression for a negative feedback amplifier given by

$A_{FB}={\frac {A_{OL}}{1+\beta A_{OL}}}\ ,$

where A_FB is the gain of the amplifier with feedback (the closed-loop gain), β is the feedback factor and A_OL is the gain without feedback (the open-loop gain). The gain A_OL is a complex function of frequency, with both magnitude and phase. Examination of this relation shows the possibility of infinite gain (interpreted as instability) if the product βA_OL = −1. (That is, the magnitude of βA_OL is unity and its phase is −180°, the so-called Barkhausen criteria). Bode plots are used to determine just how close an amplifier comes to satisfying this condition.

Key to this determination are two frequencies. The first, labeled here as f₁₈₀, is the frequency where the open-loop gain flips sign. The second, labeled here f_0dB, is the frequency where the magnitude of the product | β A_OL | = 1 (in dB, magnitude 1 is 0 dB). That is, frequency f₁₈₀ is determined by the condition:

$\beta A_{OL}\left(f_{180}\right)=-|\beta A_{OL}\left(f_{180}\right)|=-|\beta A_{OL}|_{180}\ ,$

where vertical bars denote the magnitude of a complex number (for example, | a + j b | = [ a² + b²]^1/2 ), and frequency f_0dB is determined by the condition:

$|\beta A_{OL}\left(f_{0dB}\right)|=1\ .$

One measure of proximity to instability is the gain margin. The Bode phase plot locates the frequency where the phase of βA_OL reaches −180°, denoted here as frequency f₁₈₀. Using this frequency, the Bode magnitude plot finds the magnitude of βA_OL. If |βA_OL|₁₈₀ = 1, the amplifier is unstable, as mentioned. If |βA_OL|₁₈₀ < 1, instability does not occur, and the separation in dB of the magnitude of |βA_OL|₁₈₀ from |βA_OL| = 1 is called the gain margin. Because a magnitude of one is 0 dB, the gain margin is simply one of the equivalent forms: 20 log₁₀( |βA_OL|₁₈₀) = 20 log₁₀( |A_OL|₁₈₀) − 20 log₁₀( 1 / β ).

Another equivalent measure of proximity to instability is the phase margin. The Bode magnitude plot locates the frequency where the magnitude of |βA_OL| reaches unity, denoted here as frequency f_0dB. Using this frequency, the Bode phase plot finds the phase of βA_OL. If the phase of βA_OL( f_0dB) > −180°, the instability condition cannot be met at any frequency (because its magnitude is going to be < 1 when f = f₁₈₀), and the distance of the phase at f_0dB in degrees above −180° is called the phase margin.

If a simple yes or no on the stability issue is all that is needed, the amplifier is stable if f_0dB < f₁₈₀. This criterion is sufficient to predict stability only for amplifiers satisfying some restrictions on their pole and zero positions (minimum phase systems). Although these restrictions usually are met, if they are not another method must be used, such as the Nyquist plot.

(PD) Image: John R. Brews
Gain of feedback amplifier A_FB in dB and corresponding open-loop amplifier A_OL. The gain margin in this amplifier is nearly zero because βA_OL = 1 occurs at almost f = f_180°.

(PD) Image: John R. Brews
Phase of feedback amplifier °A_FB in degrees and corresponding open-loop amplifier °A_OL. The phase margin in this amplifier is nearly zero because the phase-flip occurs at almost the unity gain frequency f = f_0dB where βA_OL = 1.

Examples using Bode plots

Two examples illustrate gain behavior and terminology. For a three-pole amplifier, gain and phase plots for a borderline stable and a stable amplifier are compared.

Borderline stable amplifier

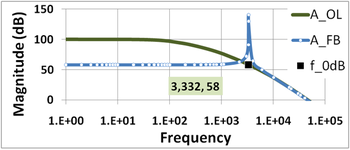
The first of two figures at the right compares the Bode plots for the gain without feedback (the open-loop gain) A_OL with the gain with feedback A_FB (the closed-loop gain). See negative feedback amplifier for more detail.

Because the open-loop gain A_OL is plotted and not the product β A_OL, the condition {{{1}}} decides the frequency where {{{1}}} that is the frequency labeled f_0dB. The feedback gain at low frequencies and for large A_OL is A_FB ≈ 1 / β (look at the formula for the feedback gain at the beginning of this section for the case of large gain A_OL), so an equivalent way to find f_0dB is to look where the feedback (or closed-loop) gain intersects the open-loop gain. (Frequency f_0dB is needed later to find the phase margin.)

Near the crossover of the two gains at f_0dB, the Barkhausen criteria are almost satisfied in this example, and the feedback amplifier exhibits a massive peak in gain (it would be infinity if {{{1}}} Beyond the unity gain frequency f_0dB, the open-loop gain is sufficiently small that A_FB ≈ A_OL (examine the formula at the beginning of this section for the case of small A_OL).

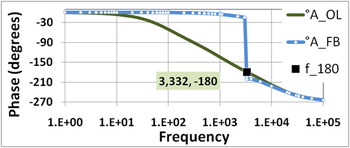
The second of the two figures shows the corresponding phase comparison: the phase of the feedback amplifier is nearly zero out to the frequency f₁₈₀ where the open-loop gain has a phase of −180°. In this vicinity, the phase of the feedback amplifier plunges abruptly downward to become almost the same as the phase of the open-loop amplifier. (Recall, A_FB ≈ A_OL for small A_OL.)

Comparing the labeled points in these two figures, it is seen that the unity gain frequency f_0dB and the phase-flip frequency f₁₈₀ are very nearly equal in this amplifier, f₁₈₀ ≈ f_0dB ≈ 3.332 kHz, which means the gain margin and phase margin are nearly zero. The amplifier is borderline stable.

Stable example

(PD) Image: John R. Brews
Gain of feedback amplifier A_FB in dB and corresponding open-loop amplifier A_OL. The gain margin in this amplifier is 19 dB.

(PD) Image: John R. Brews
Phase of feedback amplifier A_FB in degrees and corresponding open-loop amplifier A_OL. The phase margin in this amplifier is 45°.

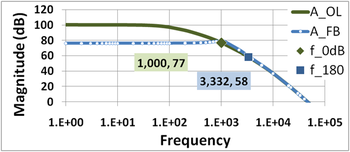
The last two figures on the right illustrate the gain margin and phase margin for a different amount of feedback β. The feedback factor is chosen smaller than in previous borderline stable amplifier, moving the the condition | β A_OL | = 1 to the lower frequency of f_0dB = 1 kHz.

The upper of the two figures shows the gain plot. The intersection of 1 / β and A_OL occurs at f_0dB = 1 kHz. Notice that the peak in the gain A_FB near f_0dB seen in the borderline stable amplifier is almost gone.

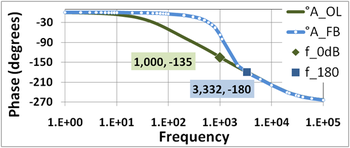
The lower of the two figures is the phase plot. Using the value of f_0dB = 1 kHz found above from the magnitude plot, the open-loop phase at f_0dB is −135°, which is a phase margin of 45° above −180°.

Using the phase plot, for a phase of −180° the value of f₁₈₀ = 3.332 kHz (the same result as found earlier, of course). The open-loop gain from the gain plot at f₁₈₀ is 58 dB, and 1 / β = 77 dB, so the gain margin is 19 dB.

As an aside, it should be noted that stability is not the sole criterion for amplifier response, and in many applications a more stringent demand than stability is good step response. As a rule of thumb, good step response requires a phase margin of at least 45°, and often a margin of over 70° is advocated, particularly where component variation due to manufacturing tolerances is an issue. See also the discussion of phase margin in the step response article.