Schottky diode

(PD) Image: John R. Brews
Planar Schottky diode with n⁺-guard rings and tapered oxide.

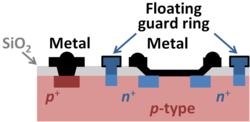
The Schottky diode is a two-terminal device consisting of conductive gate (for example, a metal) on top of a semiconductor body. A generic name for this structure is the metal-semiconductor diode or M/S diode. For low voltage applications, below 200V, silicon is used, but for higher voltages (up to 3000 V or more) silicon carbide is used to extend the breakdown voltage. These voltages are achievable only when edge breakdown is avoided, which requires special attention to edge termination designs. The figure shows three strategies toward increasing the edge breakdown voltage: an extension of the metal diode contact over a tapered oxide and also an n⁺-guard ring and a floating guard ring. These strategies are sometimes used together, but also are used separately. The substrate contact is made through an ohmic contact to the p-substrate made using a metal-to-p⁺ region on the surface of the diode.

Applications

The Schottky diode is used in a large variety of applications, ranging from practical devices for switching, rectification and photo-detection, to test structures for fabrication monitoring and for studies of semiconductor defects and processes.

(PD) Image: John R. Brews
Comparison of Schottky and pn-diode current voltage curves.

Operation

Three different bias cases are examined: zero bias, forward bias, and reverse bias. A simplified one dimensional analysis along a line vertically through the center of the Schottky contact is used throughout. It is imagined that the p⁺-ohmic contact is vertically below the Schottky contact.

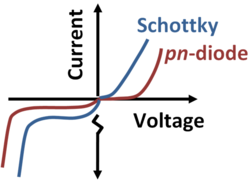
As seen in the comparison with the pn-diode shown in the figure, the Schottky diode tends to turn on at lower forward voltages but rises more slowly because of the nonideality factor noted later. The Schottky diode also tends to have a higher reverse leakage current.

(PD) Image: John R. Brews
Schottky barrier formation on p-type semiconductor. Energies are in eV.

Zero bias

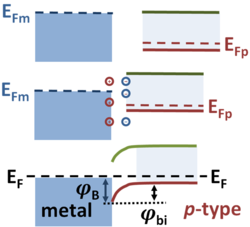
The figure shows (top) a charge-neutral, partly filled metal energy band and a charge-neutral semiconductor valence and conduction band, electrically isolated from each other. The Fermi level in the p-type semiconductor E_Fp (assumed to be in units of eV) is near its valence band edge, as set by its acceptor impurity doping. (See Fermi level). The Fermi level in the metal E_Fm marks the top of the filled electron energy levels in a partly filled band of the metal.

Ordinarily, the Fermi levels of different materials differ. When they are brought into electrical contact, enabling electron transfer between the materials, the work done in removing an electron from one material and placing it in the other is equal to the energy difference in the Fermi levels. Consequently, energy is released upon contact by electron transference from the material with the higher Fermi level to the material with the lower Fermi level. This charge transfer continues until the electrical charge difference means the energy gain from transfer is countered by the electrical work required against the charge difference. At this point the two Fermi levels are brought into coincidence at a common level E_F (bottom panel in the figure) and no further charge transfer occurs. This flat Fermi level situation corresponds to thermal equilibrium, and no net current flows once equilibrium is reached.

It should be noted that it is simplistic to suggest that it is the properties of the bulk materials by themselves that determine the charge transfer between them. In fact, the chemistry of the interface, defects at the interface, and the mechanical adaptation to new atomic positions near the interface that are differently spaced than those found in bulk material, all conspire to alter the amount of charge transfer from that expected from bulk properties.

Interfacial chemistry within a few nm of the interface may introduce localized charge dipoles that affect the amount of charge transfer. But, in any case, charge transfer occurs and the two materials each acquire a charge. In the example shown in the figure, the metal loses electrons and forms an extremely thin positive charge layer near the interface. The semiconductor gains electrons, as indicated by the bending of the valence band edge away from the Fermi level, which increases the valence band occupancy by electrons. Differently stated, the vacancies (holes) in the valence band are reduced in number, and the charge balance in the band-bending region is lost. In this depletion layer, the holes or majority carriers are depleted, exposing the immobile negative acceptor dopant ions to make this region charge-negative, and this charge results in a potential according to Poisson's equation. The potential decreases with distance toward the bulk semiconductor, and at some distance (the depletion width) the bulk properties of the semiconductor are regained and the semiconductor bulk is charge neutral.

The resulting potential drop across the semiconductor depletion layer is called the Schottky barrier height, labeled φ_B in the figure. It is a form of contact potential.

(PD) Image: John R. Brews
Under forward bias V_F the Schottky barrier height is reduced and the Fermi levels are split.

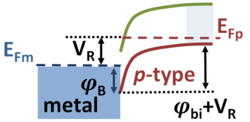
Forward bias

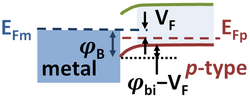
If a forward bias voltage is applied V_F, the Fermi level of the bulk metal E_Fm (in eV) is raised in energy above the bulk Fermi level in the semiconductor E_Fp, which lowers the Schottky barrier height to a value φ_B−V_F. A current of holes now flows from the semiconductor to the metal (or, equivalently, of electrons from the metal to the semiconductor). Notice that the alignment of the metal Fermi level relative to the semiconductor band edges is not changed by the bias: that is fixed by the processes involved in adjusting the Fermi levels to achieve equilibrium at zero applied bias.

A current flows under forward bias. According to the model of thermionic emission, the electrical current flowing through the semiconductor is proportional to the hole density on either side the interface. At zero bias there is no current, because the current from the semiconductor is balanced by that from the metal. But under forward bias the current from the metal side is unaffected (and extremely small), while that on the semiconductor side is increased by the forward bias. Using a simple Boltzmann approximation to the Fermi function, the hole density on the semiconductor side is increased by a factor:

$p(V_{F})=p(0)e^{qV_{F}/k_{B}T}\ ,$

where p(0) is the zero forward bias value of hole density on the semiconductor side. The hole current from the semiconductor to the metal therefore is increased by this factor. The current, being by convention a flow of positive charge, is therefore positive from the semiconductor to the metal, and the Schottky barrier current in forward bias becomes:

$I(V_{F})=I(0)\left(e^{qV_{F}/k_{B}T}-1\right)\ .$

Due to some complications of real Schottky barriers, the current is usually represented as:

$I(V_{F})=I(0)\left(e^{qV_{F}/nk_{B}T}-1\right)\ ,$

where the factor n is usually larger than one and is called the ideality factor.

(PD) Image: John R. Brews
Schottky diode under reverse bias V_R.

Reverse bias

If a reverse bias V_R is applied, the Fermi level of the metal is lowered below that of the semiconductor, and the barrier height for holes is increased on the semiconductor side by the amount of the reverse bias. The hole density is therefore decreased compared to equilibrium (the electron occupancy increases) and the current from the semiconductor falls below the equilibrium value. That means the diode current changes direction compared to the forward biased case.

In reverse bias a leakage current is drawn due to generation of electrons and holes by defects in the depletion layer. If a large enough reverse voltage is applied, breakdown occurs, due to runaway of the generation mechanisms, or more commonly, due to edge breakdown in the high field region near the contact perimeter.

Unlike the MOSFET or the MOS capacitor, the expansion of the depletion layer width in response to an applied reverse bias is not arrested at large biases by formation of an inversion layer, a layer of minority carriers (electrons in a p-type semiconductor). An inversion layer cannot form, because the carriers are transmitted to the metal, and cannot be stored at the interface.