Tetration/Code/HolomorphicBaseSqrt2v01: Difference between revisions
Jump to navigation
Jump to search
imported>Dmitrii Kouznetsov mNo edit summary |
imported>Chris Day |
Revision as of 23:38, 18 February 2009
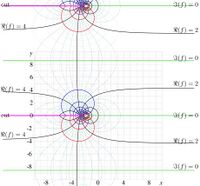
// Generator of the eps version of plot ot holomorphic tetration at base
in the compex plane
// The following graphical functions are required to compile it:
// ContourPlot/code/ado.cin
// ContourPlot/code/conto.cin
// Copyleft 2008 by Dmitrii Kouznetsov
#include <math.h>
#include <stdio.h>
#include <stdlib.h>
#define DB double
#define DO(x,y) for(x=0;x<y;x++)
#include <complex.h>
#define z_type complex<double>
#define Re(x) x.real()
#define Im(x) x.imag()
#define I z_type(0.,1.)
#include "conto.cin"
main(){ int j,k,m,n; DB x,y, p,q, t; z_type z,c,d, cu,cd;
int K=200,K1=K+1;
DB A=10.; DB dy=2*A/K; printf("dy=%6.3f",dy);
#define Y(k) (dy*(k-K/2))
printf("y_0=%6.3f y_K=%6.3f ",Y(0), Y(K));
int M=300,M1=M+1;
int N=300,N1=N+1;
DB X[M1],Y[N1], g[M1*N1],f[M1*N1], w[M1*N1]; // w is working array.
char v[M1*N1]; // v is working array
FILE *o;o=fopen("TetrationBaseSqrt2v01.eps","w");ado(o,0,0,304,404);
fprintf(o,"152 202 translate\n 10 10 scale\n");
DB sy=20./(N/2.);
DO(m,M1) X[m]=-15+.1*m;
DO(n,N1) Y[n]=sy*(n-N/2.+.5);
for(m=-10;m<11;m++) {M(m,-10)L(m,10)}
for(n=-10;n<11;n++) {M( -10,n)L(10,n)} fprintf(o,".006 W 0 0 0 RGB S\n");
fprintf(o,"/adobe-Roman findfont 1 scalefont setfont\n");
//fprintf(o,"/times-Roman findfont 1 scalefont setfont\n");
for(m=-8;m<0;m+=2) {M(-11.2,m-.3) fprintf(o,"(%1d)s\n",m);}
for(m=0;m<9;m+=2) {M(-10.7,m-.3) fprintf(o,"(%1d)s\n",m);}
for(m=-8;m<0;m+=4) {M(m-.6,-10.8) fprintf(o,"(%1d)s\n",m);}
for(m= 0;m<9;m+=4) {M(m-.3,-10.8) fprintf(o,"(%1d)s\n",m);}
fprintf(o,"/Times-Italic findfont 1 scalefont setfont\n");
//fprintf(o,"/adobe-italic findfont 1 scalefont setfont\n");
M( 9.6,-10.8) fprintf(o,"(y)s\n");
M(-10.7, 9.5) fprintf(o,"(x)s\n");
M(-11,0)L(11,0)
M (0,-11)L(0,11) fprintf(o,".01 W 1 0 1 RGB S\n");
z_type tm,tp,F[M1*N1];;
DO(m,M1)DO(n,N1){g[m*N1+n]=999; f[m*N1+n]=999; }
for(m=M-10;m<M1;m++){ x=X[m]; int m1;
DO(n,N1){y=Y[n]; z=z_type(x,y);
c=2.-exp(-0.36651292058166432701*z-.456);
m1=m;
for(;m1>0;){ F[m1*N1+n]=c; p=Re(c); q=Im(c);
if(p>-999 && p<999) g[m1*N1+n]=p;
if(q>-999 && q<999) f[m1*N1+n]=q;
c=log(c)/log(sqrt(2.)); m1-=10;
}
}
}
p=.8;
conto(o,f,w,v,X,Y,M,N, (-5. ),-1,1); fprintf(o,".06 W 1 0 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N, (-4. ),-2,2); fprintf(o,".06 W 1 0 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N, (-3. ),-p,p); fprintf(o,".06 W 1 0 0 RGB S\n");
for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N, (-3.+.1*n),-.1,.1); fprintf(o,".01 W 0 1 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N, (-2. ),-2,2); fprintf(o,".06 W 1 0 0 RGB S\n");
for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N, (-2.+.1*n),-p,p); fprintf(o,".01 W 0 1 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N, (-1. ),-p,p); fprintf(o,".06 W 1 0 0 RGB S\n");
for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N, (-1.+.1*n),-.1,.1); fprintf(o,".01 W 0 1 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N, (0. ),-p,p); fprintf(o,".06 W 0 .8 0 RGB S\n");
for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N, ( .1*n),-.1,.1); fprintf(o,".01 W 0 1 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N, ( 1. ),-p,p); fprintf(o,".06 W 0 0 1 RGB S\n");
for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N, ( 1.+.1*n),-.1,.1); fprintf(o,".01 W 0 1 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N, ( 2. ),-2,2); fprintf(o,".06 W 0 0 1 RGB S\n");
for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N, ( 2.+.1*n),-p,p); fprintf(o,".01 W 0 1 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N, ( 3. ),-2,2); fprintf(o,".06 W 0 0 1 RGB S\n");
for(n=2;n<10;n+=2)conto(o,f,w,v,X,Y,M,N, ( 3.+.1*n),-.1,.1); fprintf(o,".01 W 0 1 0 RGB S\n");
conto(o,f,w,v,X,Y,M,N, ( 4. ),-2,2); fprintf(o,".06 W 0 0 1 RGB S\n");
conto(o,f,w,v,X,Y,M,N, ( 5. ),-1,1); fprintf(o,".06 W 0 0 1 RGB S\n");
//
conto(o,g,w,v,X,Y,M,N, (-2. ),-3,3); fprintf(o,".06 W 0 0 0 RGB S\n");
for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N, (-2.+.1*n),-p,p); fprintf(o,".01 W 1 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, (-1. ),-3,3); fprintf(o,".06 W 0 0 0 RGB S\n");
for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N, (-1.+.1*n),-p,p); fprintf(o,".01 W 1 0 0 RGB S\n");
conto(o,g,w,v,X,Y,M,N, (0. ),-3,3); fprintf(o,".06 W 0 0 0 RGB S\n");
for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N, ( .1*n),-p,p); fprintf(o,".01 W 0 0 1 RGB S\n");
conto(o,g,w,v,X,Y,M,N, ( 1. ),-3,3); fprintf(o,".06 W 0 0 0 RGB S\n");
for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N, ( 1.+.1*n),-p,p); fprintf(o,".01 W 0 0 1 RGB S\n");
conto(o,g,w,v,X,Y,M,N, ( 2. ),-3,3); fprintf(o,".06 W 0 0 0 RGB S\n");
for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N, ( 2.+.1*n),-p,p); fprintf(o,".01 W 0 0 1 RGB S\n");
conto(o,g,w,v,X,Y,M,N, ( 3. ),-3,3); fprintf(o,".06 W 0 0 0 RGB S\n");
for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N, ( 3.+.1*n),-p,p); fprintf(o,".01 W 0 0 1 RGB S\n");
conto(o,g,w,v,X,Y,M,N, ( 4. ),-3,3); fprintf(o,".06 W 0 0 0 RGB S\n");
for(n=2;n<10;n+=2)conto(o,g,w,v,X,Y,M,N, ( 4.+.1*n),-p,p); fprintf(o,".01 W 0 0 1 RGB S\n");
conto(o,g,w,v,X,Y,M,N, ( 5. ),-2,2); fprintf(o,".06 W 0 0 0 RGB S\n");
//
fprintf(o,"showpage\n\%\%\%Trailer"); fclose(o);
//system( "ggv TetrationBaseSqrt2v01.eps"); // for unix
system("open TetrationBaseSqrt2v01.eps"); //for macintosh
system("ps2pdf TetrationBaseSqrt2v01.eps");
getchar(); system("killall Preview"); //for macintosh
}
// end of TetrationBaseSqrt2v01.cc //