Factorial: Difference between revisions
imported>Richard Pinch (subpages) |
imported>Dmitrii Kouznetsov (add figure) |
||
| Line 24: | Line 24: | ||
:<math> n! \approx \sqrt{2\pi} n^{n+1/2} e^{-n} . \,</math> | :<math> n! \approx \sqrt{2\pi} n^{n+1/2} e^{-n} . \,</math> | ||
==Inverse funciton== | |||
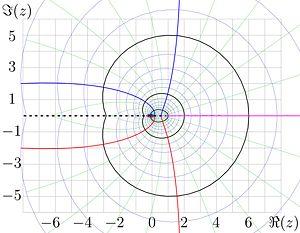
[[Image:ArcGamma.jpg|300px|right|thumb|ArcFactorial in the complex plane.]] | |||
Inverse function of factorial can be defined with equation | |||
:<math>(\mathrm{ArcFactorial}(z))!=1</math> | |||
and condition that ArcFactorial is [[holomorphic]] in the comlex plane with cut along the part of the real axis, that begins at the minimum of factorial of the real argument and extends to <math>-\infty</math>. This function is shown with | |||
lines of constant real part <math>u=\Re(\mathrm{ArcFactorial}(z))</math> and | |||
lines of constant imaginary part <math>u=\Re(\mathrm{ArcFactorial}(z))</math>. | |||
Levels <math>u=1,2,3</math> are shown with thick black curves.<br> | |||
Levels <math>u= | |||
0.2,0.4,0.6,0.8, | |||
1.2,1.4,1.6,1.8, | |||
2.2,2.4,2.6,2.8, | |||
3.2,3.4,3.6 </math> are shown with thin blue curves.<br> | |||
Levels <math>v=1,2,3</math> are shown with thick blue curves.<br> | |||
Level <math>v=0</math> is shown with thick pink line.<br> | |||
Levels <math>v=-1,-2,-3</math> are shown with thick red curves.<br> | |||
The intermediate levels of constant <math>v</math> are shown with thin dark green curves. | |||
The ArcFactorial has the [[branch point]] <math>z_0</math>\approx 0.85 </math>; the cut of the range of holomorphizm is shown with black dashed line. | |||
The figure shows the mapping ot the complex plain with the factorial function. In particular, factorial maps the unity to unity; | |||
two is mapped to two, and 3 is mapped to 6. | |||
==References== | ==References== | ||
* {{cite book | author=Ronald L. Graham | coauthors=Donald E. Knuth, Oren Patashnik | title=Concrete Mathematics | publisher=[[Addison Wesley]] | year=1989 | isbn=0-201-14236-8 | pages=111,332 }} | * {{cite book | author=Ronald L. Graham | coauthors=Donald E. Knuth, Oren Patashnik | title=Concrete Mathematics | publisher=[[Addison Wesley]] | year=1989 | isbn=0-201-14236-8 | pages=111,332 }} | ||
Revision as of 09:08, 18 January 2009
In mathematics, the factorial function gives the number of ways in which n labelled objects (for example the numbers from 1 to n) can be arranged in order. These are the permutations of the set of objects. The function is denoted by n!.
The factorial can be defined by a recurrence relation. If n labelled objects have to be assigned to n places, then the n-th object can be placed in one of n places: the remaining n-1 ojects then have to be placed in the remaining n-1 places, and this is the same problem for the smaller set. So we have
and it follows that
which we could derive directly by noting that the first element can be placed in n ways, the second in n-1 ways, and so on until the last element can be placed in only one remaining way.
Since zero objects can be arranged in just one way ("do nothing") it is conventional to put 0! = 1.
The factorial function is found in many combinatorial counting problems. For example, the binomial coefficients, which count the number of subsets size r drawn from a set of n objects, can be expressed as
The factorial function can be extended to arguments other than positive integers: this gives rise to the Gamma function.
Stirling's formula
For large n there is an approximation due to Scottish mathematician James Stirling
Inverse funciton
Inverse function of factorial can be defined with equation
and condition that ArcFactorial is holomorphic in the comlex plane with cut along the part of the real axis, that begins at the minimum of factorial of the real argument and extends to . This function is shown with lines of constant real part and lines of constant imaginary part .
Levels are shown with thick black curves.
Levels are shown with thin blue curves.
Levels are shown with thick blue curves.
Level is shown with thick pink line.
Levels are shown with thick red curves.
The intermediate levels of constant are shown with thin dark green curves.
The ArcFactorial has the branch point \approx 0.85 </math>; the cut of the range of holomorphizm is shown with black dashed line.
The figure shows the mapping ot the complex plain with the factorial function. In particular, factorial maps the unity to unity; two is mapped to two, and 3 is mapped to 6.
References
- Ronald L. Graham; Donald E. Knuth, Oren Patashnik (1989). Concrete Mathematics. Addison Wesley, 111,332. ISBN 0-201-14236-8.