Elliptic curve

An elliptic curve over a field $K$ is a one dimensional Abelian variety over $K$. Alternatively it is a smooth algebraic curve of genus one together with marked point.

Curves of genus 1 as smooth plane cubics

If $f(x,y,z)$ is a homogenous degree 3 (also called "cubic") polynomial in three variables, such that at no point $(x:y:z)\in \mathbb {P} ^{2}$ all the three derivatives of f are simultaneously zero, then the Null set $E:=\{(x:y:z)\in \mathbb {P} ^{2}|f(x,y,z)=0\}\subset \mathbb {P} ^{2}$ is a smooth curve of genus 1. Smoothness follows from the condition on derivatives, and the genus can be computed in various ways; e.g.:

• Let $H$ be the class of line in the Picard group $Pic(P^{2})$, then $E$ is rationally equivalent to $3H$. Then by the adjunction formula we have $\#K_{E}=(K_{\mathbb {P} ^{2}}+[E])[E]=(-3H+3H)3H=0$.
• By the genus-degree formula for plane curves we see that $genus(E)=(3-1)(3-2)/2=1$
• If we choose a point $p\in E$ and a line $L\subset \mathbb {P} ^{2}$ such that $p\not \in L$, we may project $E$ to $L$ by sending a point $q\in E$ to the intersection point ${\overline {pq}}\cap L$ (if $p=q$ take the line $T_{p}(E)$ instead of the line ${\overline {pq}}$). This is a double cover of a line with four ramification points. Hence by the Riemann-Hurwitz formula $genus(E)-1=-2+4/2=0$

On the other hand, if $C$ is a smooth algebraic curve of genus 1, and $p,q,r$ are points on $C$, then by the Riemann-Roch formula we have $h^{0}(O_{C}(p+q+r))=3-(1-1)-h^{0}(-(p+q+r))=3.$. Choosing a basis $g_{0},g_{1},g_{2}$ to the three dimensional vector space $H^{0}(O_{C}(p+q+r))=\{g:C\to \mathbb {P} ^{1}$ such that $g$ is algebraic and $g^{-1}(\infty )=\{p,q,r\}\}$, the map given by $s\in C\mapsto (g_{0}(s):g_{1}(s):g_{2}(s))\in \mathbb {P} ^{2}$ is an embedding.

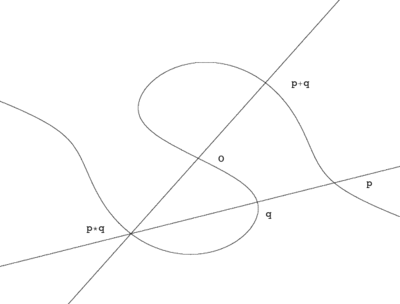
The group operation on a pointed smooth plane cubic

Addition on cubic with a marked point $O$

Let $E$ be as above, and $O$ point on $E$. If $p$ and $q$ are two points on $E$ we set $p*q:={\overline {pq}}\cap E\setminus \{p,q\},$ where if $p=q$ we take the line $T_{p}(E)$ instead, and the intersection is to be understood with multiplicities. The addition on the elliptic curve $E$ is defined as $p+q:=O*(p*q)$. Both the commutativity and the existence of inverse follow from the definition. The proof of the associativity of this operation is more delicate.

Weierstrass forms

If the cubic curve $E$ admits a flex - i.e. a line $l$ which is tri-tangent to $E$ at a point $p$ (this happens e.g. if the field $K$ is algebraically closed), then by a change of coordinates on the projective plane, which takes the line $l$ to the line $\{z=0\}$ and the point $p$ to the point $(0:1:0)$ we may assume that the only terms in the cubic polynomial $f$ which include $y$, are $y^{2}z,xyz,yz^{2}$.

If the characteritic of $K$ is not 2 or 3 then by another change of coordinates, the cubic polynomial can be changed to the form $y^{2}=x^{3}-27c_{4}x-54c_{6}$. In this case the discriminant of the cubic polynomial on the left hand side of the equation is given by $\Delta =(c_{4}^{3}-c_{6}^{2})/1728$. The $j$ invariant of the curve $E$ is defined to be $c_{4}^{3}/\Delta$. Two elliptic curves are isomorphic if and only if they have the same $j$ invariant.

Elliptic curves over the complex numbers

One dimensional complex tori and lattices in the complex numbers

An elliptic curve over the complex numbers is a Riemann surface of genus 1, or a two dimensional torus over the real numbers. The universal cover of this torus, as a complex manifold, is the complex line $\mathbb {C}$. Hence the elliptic curve is isomorphic to a quotient of the complex numbers by some lattice; moreover two elliptic curves are isomorphic if and only the two corresponding lattices are isomorphic. Hence the moduli of elliptic curves over the complex numbers is identified with the moduli of lattices in $\mathbb {C}$ up to homothety. For each homothety class there is a lattice such that one of the points of the lattice is 1, and the other is some point $\tau$ in the upper half plane ${\mathcal {H}}$.

Each triangular region is a free regular set of ${\mathcal {H}}/SL_{2}(\mathbb {Z} )$;; the grey one (with the third point of the triangle at infinity) is the canonical fundamental domain.

Hence the moduli of lattices in $\mathbb {C}$ is the quotient ${\mathcal {H}}/PSL_{2}(\mathbb {Z} )$, where a group element

$\left({\begin{matrix}a&b\\c&d\end{matrix}}\right)\in SL_{2}(\mathbb {Z} )$ acts on the upper half plane via the mobius transformation $z\mapsto {\frac {az+b}{cz+d}}$. The standard fundamental domain for this action is the set: $\{\tau |-{\frac {1}{2}}\leq Im(\tau )\leq {\frac {1}{2}},|\tau |\geq 1\}$.

Modular forms

For the main article see Modular forms Modular forms are functions on the upper half plane, such that for any $\gamma =\left({\begin{matrix}a&b\\c&d\end{matrix}}\right)\in SL_{2}(\mathbb {Z} )$ we have $f(\gamma (\tau ))=(c\tau +d)^{k}f(\tau )$ for some $k$ which is called the "weight" of the form.

Theta functions

For the main article see Theta function

Weierstrass's $\wp$ function

Let $\Lambda =\omega _{1}\mathbb {Z} +\omega _{2}\mathbb {Z}$ be a lattice. The Weirstrass $\wp$-function is the absolutely convergent series $\wp (z,\Lambda )={\frac {1}{z^{2}}}+\sum _{\omega \in \Lambda }'{\frac {1}{(z-\omega )^{2}}}-{\frac {1}{\omega ^{2}}}$ where the sum is taken over all nonzero lattice points. It is an elliptic function having poles of order two at each lattice point.

Selected references

Further reading

• Joseph H. Silverman, John Tate; "Rational Points on Elliptic Curves". ISBN 0387978259.
• Joseph H. Silverman "The Arithmetic of Elliptic Curves" ISBN 0387962034

Selected external links

• Mathematics site by J.S. Milne