Equator: Difference between revisions
imported>Paul Wormer (→Earth) |
imported>Paul Wormer (→Earth) |
||
| (6 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
{{subpages}} | {{subpages}} | ||
An '''equator''' is an imaginary circle on the surface of a rotating [[sphere]]. As any three-dimensional object, a sphere rotates around a line through its mass center; this line is known as ''rotation axis''. In absence of external [[torque]]s, a rotation axis is fixed in space. The two places where the rotation axis intersects the surface of the sphere are the ''poles'' (the [[North Pole]] and the [[South Pole]]). The '''equator''' is defined as the intersection | An '''equator''' is an imaginary circle on the surface of a rotating [[sphere]]. As any three-dimensional object, a sphere rotates around a line through its mass center; this line is known as ''rotation axis''. In absence of external [[torque]]s, a rotation axis is fixed in space. The two places where the rotation axis intersects the surface of the sphere are the ''poles'' (the [[North Pole]] and the [[South Pole]]). The '''equator''' is defined as the intersection of the surface of the sphere with a plane (the ''equatorial plane'') that passes through the center of the sphere and is orthogonal to its rotation axis. The equator is a [[great circle]], that is, its center coincides with the center of the sphere. Clearly the equator is midway between the poles and divides the sphere exactly into two halves, the [[Northern hemisphere|Northern]] and [[Southern hemisphere]], hence the name (literally equator means divider in equal parts, hemi [ἡμι] is Greek for half). Note that usually the term hemisphere denotes the surface of the half-sphere, not the half-sphere itself. | ||
==Earth== | ==Earth== | ||
{{Image|Equator.png|right|250px|}} | {{Image|Equator.png|right|250px|}} | ||
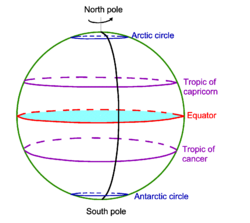
The [[Earth]] is | The [[Earth]] is the sphere for which the concept of equator is most important. On Earth the equator services as a reference for [[geographical coordinates]]. It is the zero of [[latitude]], i.e., the equator has by definition zero degrees (0°) latitude, the North Pole has by definition ninety degrees latitude (90°N) and the South Pole has latitude 90°S. | ||
In 1980 the Earth's equatorial radius was fixed to a reference value nearest to the meter (6 378 137 m) by the [[International Union of Geodesy and Geophysics]].<ref name="Moritz"> For computational purposes the radius and angular velocity were standardized, which involves obviously approximations as neither the meter nor the second are defined by the Earth's properties. See: H. Moritz, ''Geodetic reference system 1980'', Journal of Geodesy, | |||
Vol. '''54''', pp. 395–405 (1980). [http://dx.doi.org/10.1007/BF02521480 DOI]</ref> This gives the equatorial length equal to 40 075 017 m ≈ 40 075 km. The linear velocity (with respect to an inertial system fixed to the Sun) of a point on Earth, resulting from the diurnal rotation with its angular period of 23h 56 min,<ref name="Moritz"/> is highest on the equator and is there about 40075/23.934 ≈ 1674 km/h. Obviously, the linear velocity decreases going north or south and is zero on both poles.<ref> This is because the linear velocity ''v'' of a point on the surface of a rotating sphere is linear in the distance ''r'' of the point to the rotation axis: ''v''=ω''r'', where ω is the angular velocity of the sphere.</ref> | |||
Under the assumption that the Earth is a perfect sphere, the length of a degree of [[latitude]] and [[longitude]] give the (same) length of the equator. Measurements of the length of a longitudinal (east-west) arc became possible only around 1900 after the invention of radio telegraphy, but measurements of the length of a latitudinal (north-south) arc were already possible in antiquity and made by [[Eratosthenos]] as early as 240 BC. The first measurements of deviations from perfect sphericity were made by two French expeditions in the late 1730s, one to the arctic circle in [[Lapland]] and one to the equator in the [[Quito]] region of present-day [[Ecuador]]. Scientific members of the first expedition were [[Pierre Louis Maupertuis]], [[Alexis Claude Clairaut]], and [[Pierre Charles Le Monnier]], while [[Louis Godin]], [[Pierre Bouguer]], and [[La Condamine|Charles Marie de La Condamine]] were prominent members of the southbound expedition. Earlier the distance of arc had already been determined accurately inside France. Comparison of the data showed clearly that the Earth is an [[oblate ellipsoid]], flattened at the poles and bulging at the equator. | |||
An important circle on the Northern hemisphere (not a great circle) is the [[Tropic of Capricorn]]. This is the latitude where the Sun seems exactly overhead once a year—at the [[summer solstice]] (around June 21). In 2010 it was at 23º 26′ 17″ north of the equator (the Earth axis "wobbles" somewhat due to external torques so that the latitude varies a little in time). The [[Arctic circle]] is the [[polar circle]] 90°−23º 26′ 17″ ≈ 66° 34′ | An important circle on the Northern hemisphere (not a great circle) is the [[Tropic of Capricorn]]. This is the latitude where the Sun seems exactly overhead once a year—at the [[summer solstice]] (around June 21). In 2010 it was at 23º 26′ 17″ north of the equator (the Earth axis "wobbles" somewhat due to external torques so that the latitude of the tropic varies a little in time). The [[Arctic circle]] is the [[polar circle]] at latitude 90°−23º 26′ 17″ ≈ 66° 34′. It is the northern most latitude on Earth that just sees the sun for a very brief period above the horizon at the [[winter solstice]] (around December 22). On the Southern hemisphere these circles are called the [[Tropic of Capricorn]] and the [[Antarctic circle]], respectively. | ||
The area | The area around the equator bounded by the Tropic of Cancer and the Tropic of Capricorn, sees the Sun exactly overhead (at 90°) twice a year and at other times under an angle that deviates at most 46° from overhead position. Hence this area on Earth receives a large amount of solar energy all [[solar year|year]] round and is consequently on average the hottest region on Earth. This region (the "Tropics") hardly experiences any [[season]]s. | ||
==Sky== | ==Sky== | ||
Another important sphere is the [[celestial sphere]]. Its equatorial plane coincides with Earth's equatorial plane and the '''celestial equator''' divides the sky into a Northern and Southern sky. The celestial equatorial plane makes an angle of 23° 26' with the ecliptic. See the article [[ecliptic]] for illustrations. | Another important sphere is the [[celestial sphere]]. Its equatorial plane coincides with Earth's equatorial plane and the '''celestial equator''' divides the sky into a Northern and Southern sky. The celestial equatorial plane makes an angle of 23° 26' with the ecliptic. See the article [[ecliptic]] for illustrations. | ||
==Notes and references== | |||
<references /> | |||
Latest revision as of 09:54, 22 March 2010
An equator is an imaginary circle on the surface of a rotating sphere. As any three-dimensional object, a sphere rotates around a line through its mass center; this line is known as rotation axis. In absence of external torques, a rotation axis is fixed in space. The two places where the rotation axis intersects the surface of the sphere are the poles (the North Pole and the South Pole). The equator is defined as the intersection of the surface of the sphere with a plane (the equatorial plane) that passes through the center of the sphere and is orthogonal to its rotation axis. The equator is a great circle, that is, its center coincides with the center of the sphere. Clearly the equator is midway between the poles and divides the sphere exactly into two halves, the Northern and Southern hemisphere, hence the name (literally equator means divider in equal parts, hemi [ἡμι] is Greek for half). Note that usually the term hemisphere denotes the surface of the half-sphere, not the half-sphere itself.
Earth
The Earth is the sphere for which the concept of equator is most important. On Earth the equator services as a reference for geographical coordinates. It is the zero of latitude, i.e., the equator has by definition zero degrees (0°) latitude, the North Pole has by definition ninety degrees latitude (90°N) and the South Pole has latitude 90°S.
In 1980 the Earth's equatorial radius was fixed to a reference value nearest to the meter (6 378 137 m) by the International Union of Geodesy and Geophysics.[1] This gives the equatorial length equal to 40 075 017 m ≈ 40 075 km. The linear velocity (with respect to an inertial system fixed to the Sun) of a point on Earth, resulting from the diurnal rotation with its angular period of 23h 56 min,[1] is highest on the equator and is there about 40075/23.934 ≈ 1674 km/h. Obviously, the linear velocity decreases going north or south and is zero on both poles.[2]
Under the assumption that the Earth is a perfect sphere, the length of a degree of latitude and longitude give the (same) length of the equator. Measurements of the length of a longitudinal (east-west) arc became possible only around 1900 after the invention of radio telegraphy, but measurements of the length of a latitudinal (north-south) arc were already possible in antiquity and made by Eratosthenos as early as 240 BC. The first measurements of deviations from perfect sphericity were made by two French expeditions in the late 1730s, one to the arctic circle in Lapland and one to the equator in the Quito region of present-day Ecuador. Scientific members of the first expedition were Pierre Louis Maupertuis, Alexis Claude Clairaut, and Pierre Charles Le Monnier, while Louis Godin, Pierre Bouguer, and Charles Marie de La Condamine were prominent members of the southbound expedition. Earlier the distance of arc had already been determined accurately inside France. Comparison of the data showed clearly that the Earth is an oblate ellipsoid, flattened at the poles and bulging at the equator.
An important circle on the Northern hemisphere (not a great circle) is the Tropic of Capricorn. This is the latitude where the Sun seems exactly overhead once a year—at the summer solstice (around June 21). In 2010 it was at 23º 26′ 17″ north of the equator (the Earth axis "wobbles" somewhat due to external torques so that the latitude of the tropic varies a little in time). The Arctic circle is the polar circle at latitude 90°−23º 26′ 17″ ≈ 66° 34′. It is the northern most latitude on Earth that just sees the sun for a very brief period above the horizon at the winter solstice (around December 22). On the Southern hemisphere these circles are called the Tropic of Capricorn and the Antarctic circle, respectively.
The area around the equator bounded by the Tropic of Cancer and the Tropic of Capricorn, sees the Sun exactly overhead (at 90°) twice a year and at other times under an angle that deviates at most 46° from overhead position. Hence this area on Earth receives a large amount of solar energy all year round and is consequently on average the hottest region on Earth. This region (the "Tropics") hardly experiences any seasons.
Sky
Another important sphere is the celestial sphere. Its equatorial plane coincides with Earth's equatorial plane and the celestial equator divides the sky into a Northern and Southern sky. The celestial equatorial plane makes an angle of 23° 26' with the ecliptic. See the article ecliptic for illustrations.
Notes and references
- ↑ 1.0 1.1 For computational purposes the radius and angular velocity were standardized, which involves obviously approximations as neither the meter nor the second are defined by the Earth's properties. See: H. Moritz, Geodetic reference system 1980, Journal of Geodesy, Vol. 54, pp. 395–405 (1980). DOI
- ↑ This is because the linear velocity v of a point on the surface of a rotating sphere is linear in the distance r of the point to the rotation axis: v=ωr, where ω is the angular velocity of the sphere.