imported>Paul Wormer |
imported>Paul Wormer |
| (19 intermediate revisions by the same user not shown) |
| Line 1: |
Line 1: |
| The '''second law of [[thermodynamics]]''', as formulated in the middle of the 19th century by [[William Thomson]] (Lord Kelvin) and [[Rudolf Clausius]], states that it is impossible to gain mechanical energy (work) from heat flowing from a ''cold'' to a ''hot'' body. Clausius postulated that the opposite is the case: it requires input of mechanical (or electric) energy to transport heat from a low- to a high-temperature object. A [[heat pump]], [[air conditioner]], and [[refrigerator]] are devices that move heat from a cold to a warm place: according to Clausius they need mechanical or electric energy (work) to do it.
| | {{Image|Complex number.png|right|350px| Complex number ''z'' ≡ ''r'' exp(''i''θ) multiplied by ''i'' gives <i>z'</i> <nowiki>=</nowiki> <i>z</i>×''i'' |
| | <nowiki>=</nowiki> ''z'' exp(''i'' π/2) (counter clockwise rotation over 90°). Division of ''z'' by ''i'' gives ''z''". Division by ''i'' is multiplication by −''i'' <nowiki> = </nowiki> exp(−''i''  π/2) (clockwise rotation over 90°).}} |
|
| |
|
| Thomson formulated the second law in a slightly different, but equivalent way. He used the concept of [[heat engine]]. This is a virtual machine that converts heat into work while operating according to thermodynamic rules. Thomson postulated that it is impossible for a cyclic heat engine to receive its input from a ''single'' heat source. In a cyclic thermodynamic process, a system—such as a heat engine—ends up in a thermodynamic state that is the same as the initial state; the system has not lost or gained any [[internal energy]] after a full cycle. In order that no energy is lost in the supersystem heat-source-plus-heat-engine after a full cycle, it is necessary that the work generated by the engine is converted into heat that is returned to the heat source. According to Thomson, a heat reservoir cannot play the same role as a bank that lends money to a customer. It is not possible for a heat engine to "loan" an amount of heat from a single heat source, get work out of it, and bring back the "loaned" heat later to the same source.
| | ==Complex numbers in physics== |
| | ===Classical physics=== |
| | Classical physics consists of [[classical mechanics]], [[Maxwell's equations|electromagnetic theory]], and phenomenological [[thermodynamics]]. One can add Einstein's special and general theory of [[relativity]] to this list, although this theory, being formulated in the 20th century, is usually not referred to as "classical". In these four branches of physics the basic quantities and equations governing the behavior of the quantities are real. |
|
| |
|
| ==Discussion of the second law==
| | Classical mechanics has three different, but equivalent, formulations. The oldest, due to [[Isaac Newton|Newton]], deals with masses and position vectors of particles, which are real, as is time ''t''. The first and second time derivatives of the position vectors enter Newton's equations and these are obviously real, too. The same is true for [[Lagrange formalism|Lagrange's formulation]] of classical mechanics in terms of position vectors and velocities of particles and for [[Hamilton formalism|Hamilton's formulation]] in terms of [[momentum|momenta]] and positions. |
| If the second law would not hold, there would be no fear of energy shortage. For example, it would be possible—as already pointed out by Lord Kelvin—to propel ships by energy extracted from sea water. After all, the oceans contain immense amounts of internal energy. When one could extract just a small portion of it—whereby a slight cooling of the sea water would occur—and use this to propel a ship (a form of work), then ships could move without any net consumption of energy. It would ''not'' violate the [[first law of thermodynamics]], because the rotation of the ship's propellers would again heat the water and in total the energy of the supersystem "ship-plus-ocean" would be conserved, in agreement with the first law. Unfortunately, it is not possible, no work can be extracted from the water because it would be a single source of heat. Clausius would explain the violation of the law by observing that ships are warmer than sea water (or at least they are not colder) and hence it needs work to transport heat from the sea to the ship.
| |
|
| |
|
| {{Image|Second law.png|right|200px|''T''<sub>h</sub> > ''T''<sub>c</sub>. Second law (Kelvin): if ''W'' > 0, ''Q''<sub>c</sub> ≠ 0.}}
| | Maxwell equations, that constitute the basis of electromagnetic theory, are in terms of real vector operators ([[gradient]], [[divergence]], and [[curl]]) acting on real [[electric field|electric]] and [[magnetic field|magnetic]] fields. |
| Without the second law, one could conceive a similar setup on land where energy, extracted from the earth, would charge batteries, and heat, dissipated by electric currents generated by the batteries, would be given back to the earth. Such a device is also out of the question because the second law forbids it.
| |
|
| |
|
| The second law is summarized in the figure. Two heat reservoirs are shown, one of absolute [[temperature]] ''T''<sub>h</sub> (the hot reservoir) and the other of temperature ''T''<sub>c</sub> (the cold reservoir), ''T''<sub>h</sub> >''T''<sub>c</sub>. The reservoirs are coupled by a [[heat engine]] (green circle), a construct that converts heat ''Q''<sub>h</sub> into work ''W''. The "rest heat" ''Q''<sub>c</sub> is delivered to the cold reservoir. This idealized representation of power-generating machines was invented by [[Sadi Carnot]] who used it for the study of [[steam engine]]s. But this schematic representation applies to many machines, for instance also to an [[automobile]], a vehicle with an internal [[combustion engine]]. The high-temperature heat bath is formed by the cylinders which are hot because of the combustion of gasoline. The cold heat bath is formed by the environment of the car—the rest heat is delivered to the surroundings through the car's radiator. The cyclically moving pistons, that perform the actual work, form the heat engine.
| | Thermodynamics is concerned with concepts as [[internal energy]], [[entropy]], and [[work]]. Again, these properties are real. |
|
| |
|
| An essential feature of the process depicted in the figure is that it is reversible: all arrows may be reverted, in which case the figure represents heat flowing from cold to hot and according to Clausius work must be done by the surroundings on the system (represented by an inward arrow).
| | The special theory of relativity is formulated in [[Minkowski space]]. Although this space is sometimes described as a 3-dimensional [[Euclidean space]] to which the axis ''ict'' (''i'' is the imaginary unit, ''c'' is speed of light, ''t'' is time) is added as a fourth dimension, the role of ''i'' is non-essential. The imaginary unit is introduced as a pedestrian way to the computation of the indefinite, real, inner product that in Lorentz coordinates has the metric |
| | |
| When the heat flow is from hot to cold, work ''W'' is performed ''by'' the engine on the surroundings (outgoing ''W'' in the figure). The Kelvin principle states that ''Q''<sub>c</sub> ≠ 0, because otherwise there would be a single heat source delivering the work. Hence, the second law states that only part of the heat ''Q''<sub>h</sub> obtained from the hot reservoir, can be converted into work, the remaining part of ''Q''<sub>h</sub> is given off as the non-zero rest heat ''Q''<sub>c</sub> to the low temperature reservoir. [In the case of a car it means that only part of the combustion energy is converted into work and that the other part of the combustion energy heats up the air surrounding the car.]
| |
| | |
| It can be shown that the efficiency η ≡ ''W'' / ''Q''<sub>h</sub> is bounded:
| |
| :<math> | | :<math> |
| \eta \le \frac{T_\mathrm{h}-T_\mathrm{c}}{T_\mathrm{h}} | | \begin{pmatrix} |
| | -1 & 0 & 0 & 0 \\ |
| | 0 & 1 & 0 & 0 \\ |
| | 0 & 0 & 1 & 0 \\ |
| | 0 & 0 & 0 & 1 \\ |
| | \end{pmatrix}, |
| </math> | | </math> |
| Thus, when car cylinders operate at, say, 427 °C = 700 K and the surroundings are 27 °C = 300 K, then η ≤ 400/700 = 57%. <ref>In reality most cars run at an efficiency of about 25%, well below the thermodynamic limit.</ref> This percentage is used for driving the car, the other 43% is lost to the surroundings. It is important to note that the efficiency is limited by the second law of thermodynamics; η can only be raised by higher ''T''<sub>h</sub>, not by a better streamline of the car or other design improvements.
| | which obviously is real. In other words, Minkowski space is a space over the real field ℝ. |
| | The general theory of relativity is formulated over real [[differentiable manifold]]s that are locally Lorentzian. Further, the Einstein field equations contain mass distributions that are real. |
|
| |
|
| ==Mathematical expression of the second law==
| | So, although the classical branches of physics do not need complex numbers, this does not mean that these numbers cannot be useful. A very important mathematical technique, especially for those branches of physics where there is flow (of electricity, heat, or mass) is [[Fourier analysis]]. The Fourier series is most conveniently formulated in complex form. Although it would be possible to formulate it in real terms (expansion in terms of sines and cosines) this would be cumbersome, given the fact that the application of the usual trigonometric formulas for the multiplication of sines and cosines is so much more difficult than the corresponding multiplication of complex numbers. Especially electromagnetic theory makes heavy use of complex numbers, but it must be remembered that the final results, that are to be compared with observable quantities, are real. |
| We consider a single thermodynamic system of absolute temperature ''T'', and let ''DQ'' be a small amount of heat ''entering'' the system. In the article [[entropy]] it is proved from the Clausius/Kelvin principle that a thermodynamic system is characterized, not only by its usual parameters volume, pressure, etc., but also by the state variable ''S'', the entropy of the system. The differential ''dS'' is defined by
| | ===Quantum physics=== |
| :<math>
| | In quantum physics complex numbers are essential. In the oldest formulation, due to [[Heisenberg]] the imaginary unit appears in an essential way through the canonical commutation relation |
| dS \;\stackrel{\mathrm{def}}{=}\; \frac{DQ}{T} > 0.
| |
| </math>
| |
| When ''DQ'' leaves the system,
| |
| :<math> | | :<math> |
| dS \equiv - \frac{DQ}{T} < 0.
| | [p_i,q_j] \equiv p_i q_j - q_j p_i = -i\hbar \delta_{ij}, |
| </math>
| |
| ===Reversible processes===
| |
| The fact that entropy ''S'' is a state function implies that the following holds for a ''reversible'' cyclic process,
| |
| :<math>
| |
| \oint \frac{DQ}{T} \equiv {\int\limits_1\limits^2}_{{\!\!}^{(I)}}\frac{DQ}{T} + {\int\limits_2\limits^1}_{{\!\!}^{(II)}} \frac{DQ}{T} = \oint dS = 0 .
| |
| </math>
| |
| ''This equation is the mathematical expression of the second law of thermodynamics for the special case of reversible processes''. The cycle consists of two different paths in state space, denoted by I and II. The path integrals start and end at common points in state space, indicated by 1 and 2.
| |
| | |
| In order to show conversely that this equation yields the Clausius principle, we consider the heat engine (green circle) in the figure as our system and assume that both heat baths are so large (or the engine so small) that one full cycle of the engine does not change the temperatures of the baths. Then for one cycle of the engine one can write,
| |
| :<math>
| |
| \oint dS = \oint \frac{DQ_\mathrm{h}}{T_\mathrm{h}} - \oint \frac{DQ_\mathrm{c}}{T_\mathrm{c}} =
| |
| \frac{Q_\mathrm{h}}{T_\mathrm{h}} - \frac{Q_\mathrm{c}}{T_\mathrm{c}} = 0 \quad\qquad\qquad (1)
| |
| </math>
| |
| where we defined
| |
| :<math>
| |
| \frac{Q_\mathrm{h}}{T_\mathrm{h}} \equiv \oint \frac{DQ_\mathrm{h}}{T_\mathrm{h}} = \frac{1}{T_\mathrm{h}} \oint DQ_\mathrm{h},
| |
| </math>
| |
| and the analogous definition holds for ''Q''<sub>c</sub>. Note that from the reverse process (heat flowing from cold to hot) one obtains the same result.
| |
| | |
| By definition ''Q''<sub>h</sub> and ''Q''<sub>c</sub> are positive amounts of heat. With regard to the work ''W'', one must carefully distinguish whether work is performed ''by'' (''W''<sub>by</sub>) or ''on'' (''W''<sub>on</sub>) the system. Clearly ''W''<sub>by</sub> = −''W''<sub>on</sub>. Observe further that from equation (1) it follows that
| |
| :<math>
| |
| \frac{Q_\mathrm{h}}{Q_\mathrm{c}} = \frac{T_\mathrm{h}}{T_\mathrm{c}} > 1,
| |
| \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad(2)
| |
| </math>
| |
| i.e., ''Q''<sub>h</sub> > ''Q''<sub>c</sub> ''irrespective of the direction of the heat flow''. | |
| | |
| When the heat flow is from hot to cold (arrows are as shown in the figure), the first law states that work ''by'' the system (outward arrow) obeys the equation
| |
| :<math>
| |
| W_\mathrm{by}= Q_\mathrm{h} -Q_\mathrm{c} > 0, \, \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad(3)
| |
| </math>
| |
| that is, the heat engine performs work on its surroundings.
| |
| | |
| When the heat flow is from cold to hot (all arrows are reverted in the figure), the first law of thermodynamics states that work ''on'' the system (inward arrow) is
| |
| :<math>
| |
| W_\mathrm{on}= Q_\mathrm{h} -Q_\mathrm{c} > 0, \,
| |
| </math> | | </math> |
| meaning that the surroundings perform work ''on'' the heat engine. Hence, from the mathematical formulation of the second law follows, in correspondence with the Clausius principle, that work ''on'' the system is needed to transport heat from the cold to the hot reservoir.
| | ''p''<sub>''i''</sub> and ''q''<sub>''j''</sub> are linear operators (matrices) representing the ''i''th and ''j''th component of the momentum and position of a particle, respectively,. |
|
| |
|
| The efficiency η follows from equations (2) and (3) | | The time-dependent [[Schrödinger equation]] also contains ''i'' in an essential manner. For a free particle of mass ''m'' the equation reads |
| :<math> | | :<math> |
| \eta \equiv \frac{W_\mathrm{by}}{Q_\mathrm{h}} = \frac{Q_\mathrm{h} -Q_\mathrm{c}}{Q_\mathrm{h}}=
| | \frac{\hbar}{2m} \nabla^2 \Psi(\mathbf{r},t) = -i \frac{\partial}{\partial t} \Psi(\mathbf{r},t) . |
| 1 - \frac{Q_\mathrm{c}}{Q_\mathrm{h}} = 1 - \frac{T_\mathrm{c}}{T_\mathrm{h}} =
| |
| \frac{T_\mathrm{h}-T_\mathrm{c}}{T_\mathrm{h}},
| |
| </math> | | </math> |
| and since ''T''<sub>h</sub> > ''T''<sub>c</sub> > 0, it follows that η < 1.
| | This equation may be compared to the [[wave equation]] that appears in several branches of classical physics |
| | |
| It is good to stress that the inequality η < 1 holds for reversible processes in which there are no entropy losses. Often the fact that η is less than unity is given in the very same discussion as in which it is pointed out that entropy strives toward a maximum. It is then easy to draw the incorrect conclusion that η being less than one is solely due to entropy losses. It is true, however, that in spontaneous (irreversible) processes the entropy does increase with the consequence that the efficiency η is further reduced; the equation for η becomes an upper bound. That is, for ''irreversible processes'' the ''equality'' that is valid for reversible processes, becomes an ''inequality'',
| |
| :<math> | | :<math> |
| \eta < \frac{T_\mathrm{h}-T_\mathrm{c}}{T_\mathrm{h}}. | | v^2 \nabla^2 \Psi(\mathbf{r},t) = \frac{\partial^2}{\partial t^2} \Psi(\mathbf{r},t), |
| </math> | | </math> |
| ===Spontaneous, irreversible, processes===
| | where ''v'' is the [[phase velocity|velocity]] of the wave. It is clear from this similarity why |
| {{Image|Spontaneous process.png|right|150px|<small>Fig. 2. Upper (red) vessel contains hot fluid, lower (blue) vessel cold. The vessels have heat-conducting walls and are in a container with adiabatic walls (black).</small>}}
| | Schrödinger's equation is sometimes called the wave equation of quantum mechanics. It is also clear that the essential difference between quantum physics and classical physics is the first-order time derivative including the imaginary unit. The classical equation is real and has on the right hand side a second derivative with respect to time. |
| Many, in fact most, thermodynamic processes are spontaneous and irreversible. A well-known spontaneous process is the flow of heat from a vessel containing hot fluid to one containing cold fluid, see figure 2. The opposite process, the transport of heat from a cold to a hot vessel, needs work by the Clausius principle and is accordingly not spontaneous. The spontaneous flow of heat from hot to cold is irreversible; the terms "spontaneous" and "irreversible" will be used interchangeably in what follows.
| |
| | |
| Another example of an irreversible process is [[Count Rumford]]'s seminal cannon boring experiment in which work by a drill is converted into frictional heat. This process cannot be reverted because of the Kelvin principle. It is impossible to obtain work from the frictional heat without another, colder, reservoir present. The cannon-plus-drill forms a single source of heat.
| |
| | |
| The [[Joule-Thomson effect]] shows yet another example of an irreversible process.
| |
|
| |
|
| In figure 2 it is shown that during a certain short time span a small amount of heat ''DQ'' flows from the upper to the lower vessel, ''T''<sub>h</sub> > ''T''<sub>c</sub>. For the loss and gain of an infinitesimal amount of heat we may use the equations for the change in entropy given in the previous section. That is, the upper (hot) container loses entropy, while the lower (cold) gains entropy. For the total isolated system it holds that
| | The more general form of the Schrödinger equation is |
| :<math> | | :<math> |
| dS = -\frac{DQ}{T_\mathrm{h}} + \frac{DQ}{T_\mathrm{c}} = DQ\left( \frac{1}{T_\mathrm{c}} - \frac{1}{T_\mathrm{h}}\right) > 0.
| | H \Psi(t) = i \hbar \frac{\partial}{\partial t} \Psi(t) , |
| </math> | | </math> |
| Clearly, heat will keep on flowing until the temperature of both vessels has become equal and the entropy of the isolated system has increased ''S''<sub>2</sub> − ''S''<sub>1</sub> > 0. If the same amount of heat had been transferred from the hot to the cold reservoir, but this time reversibly through a heat engine, as in figure 1, work would have been delivered by the heat flow, while the spontaneous process of figure 2 does not perform ''any'' work. This already shows that a spontaneous process yields less work than the corresponding reversible process. This, in turn, means that the efficiency η of a spontaneous process is smaller than the efficiency of the corresponding reversible process, a result that was preluded above.
| | where ''H'' is the operator representing the energy of the quantum system under consideration. If this energy is time-independent (no time-dependent external fields interact with the system), the equation can be separated, and the imaginary unit enters fairly trivially through a so-called phase factor, |
| | |
| In order to give the formulation of the second law of thermodynamics for irreversible processes of arbitrary systems, we consider figure 3. Two paths in the state space of an arbitrary system ''C'' are depicted. The full line (path II) gives a reversible transition from state 1 to state 2, and the dashed line (path I) depicts an irreversible transition between the same two states. For the reversible path it holds that
| |
| :<math> | | :<math> |
| S_2-S_1 = \int_1^2 \frac{DQ_\mathrm{rev}}{T}.
| | \Psi(t) = e^{-iEt/\hbar} \Phi\quad\hbox{with}\quad H\Phi = E\Phi. |
| </math> | | </math> |
| It can be expected that less heat (divided by ''T'') is needed to find the same increase in entropy along the irreversible path of figure 3. Indeed, recall that figure 2 shows a spontaneous increase in entropy for which as little as zero heat was required.
| | The second equation has the form of an operator [[eigenvalue equation]]. The eigenvalue ''E'' (one of the possible observable values of the energy) is real, which is a fairly deep consequence of the quantum laws.<ref>If ''E'' were complex, two separate measurements would be necessary to determine it. One for its real and one for its imaginary part. Since quantum physics states that a measurement gives a collapse of the wave function to an undetermined state, the measurements, even if they would be made in quick succession, would interfere with each other and energy would be unobservable.</ref> The time-independent function Φ can very often be chosen to be real. The exception being the case that ''H'' is not invariant under [[time-reversal]]. Indeed, since the time-reversal operator θ is [[anti-unitary]], it follows that |
| {{Image|Cycle1.png|right|100px|<small>Fig. 3. Reversible (full) and irreversible (dashed) path in state space.</small>}}
| |
| The result follows more formally from the Kelvin principle, as will be shown now. Let system ''C'' absorb an amount of heat ''Q''<sub>irr</sub> along path I (see figure 3) that is obtained from an external heat reservoir ''R''. Let ''Q''<sub>rev</sub> be delivered by the same reservoir ''R'' to ''C'' along path II. The increase of entropy is the same along path I and II, because state 2 is independent of the path. Suppose now the opposite of the expected to hold, that is, let ''Q''<sub>irr</sub> > ''Q''<sub>rev</sub>. Path I is not reversible, but path II is. When path II is reverted the system goes through a cyclic process that receives heat ''Q''<sub>irr</sub> and delivers ''Q''<sub>rev</sub> to ''R''. Hence the heat bath ''R'' has delivered the net heat ''Q''<sub>irr</sub> − ''Q''<sub>rev</sub> > 0 after a full cycle of ''C''. When the heat exchange between ''R'' and ''C'' is mediated by a heat engine, then because of the first law and because ''C'' made a full cycle, the net heat ''Q''<sub>irr</sub> − ''Q''<sub>rev</sub> delivered by the ''single'' heat reservoir ''R'' is converted into work by the heat engine. This contradicts the Kelvin principle. Hence, | |
| :<math> | | :<math> |
| \int_1^2 \frac{dQ_\mathrm{irr}} {T} < \int_1^2 \frac{dQ_\mathrm{rev}} {T} = S_2-S_1 | | \theta H \theta^\dagger \bar{\Phi} = E \bar{\Phi} |
| </math> | | </math> |
| and the following is second law of thermodynamics for irreversible processes:
| | where the bar indicates [[complex conjugation]]. Now, if ''H'' is invariant, |
| :<math> | | :<math> |
| S_2 - S_1 > \int_1^2 \frac{dQ_\mathrm{irr}} {T}\quad\hbox{and}\quad dS > \frac{dQ_\mathrm{irr}} {T}.
| | \theta H \theta^\dagger = H \Longrightarrow H\bar{\Phi} = E\bar{\Phi}\quad\hbox{and}\quad |
| | H\Phi = E\Phi, |
| </math> | | </math> |
| | then also the real linear combination <math>\Phi+\bar{\Phi}</math> is an eigenfunction belonging to ''E'', which means that the wave function may be chosen real. If ''H'' is not invariant, it usually is transformed into minus itself. Then <math>\Phi\;</math> and <math>\bar{\Phi}</math> belong to ''E'' and −''E'', respectively, so that they are essentially different and cannot be combined to real form. Time-reversal symmetry is usually broken by magnetic fields, which give rise to interactions linear in spin or orbital [[angular momentum]]. |
|
| |
|
| ==References== | | ==Note== |
| C. S. Helrich, ''Modern Thermodynamics with Statistical Mechanics'', Springer (2009).
| |
| [http://books.google.nl/books?id=RpwpYdYmnXMC&printsec=frontcover&source=gbs_navlinks_s#v=onepage&q=&f=false Google books]
| |
| | |
| <references /> | | <references /> |
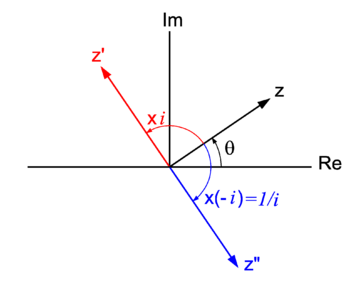
PD Image Complex number
z ≡
r exp(
iθ) multiplied by
i gives
z' =
z×
i =
z exp(
i π/2) (counter clockwise rotation over 90°). Division of
z by
i gives
z". Division by
i is multiplication by −
i = exp(−
i π/2) (clockwise rotation over 90°).
Complex numbers in physics
Classical physics
Classical physics consists of classical mechanics, electromagnetic theory, and phenomenological thermodynamics. One can add Einstein's special and general theory of relativity to this list, although this theory, being formulated in the 20th century, is usually not referred to as "classical". In these four branches of physics the basic quantities and equations governing the behavior of the quantities are real.
Classical mechanics has three different, but equivalent, formulations. The oldest, due to Newton, deals with masses and position vectors of particles, which are real, as is time t. The first and second time derivatives of the position vectors enter Newton's equations and these are obviously real, too. The same is true for Lagrange's formulation of classical mechanics in terms of position vectors and velocities of particles and for Hamilton's formulation in terms of momenta and positions.
Maxwell equations, that constitute the basis of electromagnetic theory, are in terms of real vector operators (gradient, divergence, and curl) acting on real electric and magnetic fields.
Thermodynamics is concerned with concepts as internal energy, entropy, and work. Again, these properties are real.
The special theory of relativity is formulated in Minkowski space. Although this space is sometimes described as a 3-dimensional Euclidean space to which the axis ict (i is the imaginary unit, c is speed of light, t is time) is added as a fourth dimension, the role of i is non-essential. The imaginary unit is introduced as a pedestrian way to the computation of the indefinite, real, inner product that in Lorentz coordinates has the metric

which obviously is real. In other words, Minkowski space is a space over the real field ℝ.
The general theory of relativity is formulated over real differentiable manifolds that are locally Lorentzian. Further, the Einstein field equations contain mass distributions that are real.
So, although the classical branches of physics do not need complex numbers, this does not mean that these numbers cannot be useful. A very important mathematical technique, especially for those branches of physics where there is flow (of electricity, heat, or mass) is Fourier analysis. The Fourier series is most conveniently formulated in complex form. Although it would be possible to formulate it in real terms (expansion in terms of sines and cosines) this would be cumbersome, given the fact that the application of the usual trigonometric formulas for the multiplication of sines and cosines is so much more difficult than the corresponding multiplication of complex numbers. Especially electromagnetic theory makes heavy use of complex numbers, but it must be remembered that the final results, that are to be compared with observable quantities, are real.
Quantum physics
In quantum physics complex numbers are essential. In the oldest formulation, due to Heisenberg the imaginary unit appears in an essential way through the canonical commutation relation
![{\displaystyle [p_{i},q_{j}]\equiv p_{i}q_{j}-q_{j}p_{i}=-i\hbar \delta _{ij},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/da2dc0efd4350fd14a216c592b8cc925b8a9dc4e)
pi and qj are linear operators (matrices) representing the ith and jth component of the momentum and position of a particle, respectively,.
The time-dependent Schrödinger equation also contains i in an essential manner. For a free particle of mass m the equation reads

This equation may be compared to the wave equation that appears in several branches of classical physics

where v is the velocity of the wave. It is clear from this similarity why
Schrödinger's equation is sometimes called the wave equation of quantum mechanics. It is also clear that the essential difference between quantum physics and classical physics is the first-order time derivative including the imaginary unit. The classical equation is real and has on the right hand side a second derivative with respect to time.
The more general form of the Schrödinger equation is

where H is the operator representing the energy of the quantum system under consideration. If this energy is time-independent (no time-dependent external fields interact with the system), the equation can be separated, and the imaginary unit enters fairly trivially through a so-called phase factor,

The second equation has the form of an operator eigenvalue equation. The eigenvalue E (one of the possible observable values of the energy) is real, which is a fairly deep consequence of the quantum laws.[1] The time-independent function Φ can very often be chosen to be real. The exception being the case that H is not invariant under time-reversal. Indeed, since the time-reversal operator θ is anti-unitary, it follows that

where the bar indicates complex conjugation. Now, if H is invariant,

then also the real linear combination  is an eigenfunction belonging to E, which means that the wave function may be chosen real. If H is not invariant, it usually is transformed into minus itself. Then
is an eigenfunction belonging to E, which means that the wave function may be chosen real. If H is not invariant, it usually is transformed into minus itself. Then  and
and  belong to E and −E, respectively, so that they are essentially different and cannot be combined to real form. Time-reversal symmetry is usually broken by magnetic fields, which give rise to interactions linear in spin or orbital angular momentum.
belong to E and −E, respectively, so that they are essentially different and cannot be combined to real form. Time-reversal symmetry is usually broken by magnetic fields, which give rise to interactions linear in spin or orbital angular momentum.
Note
- ↑ If E were complex, two separate measurements would be necessary to determine it. One for its real and one for its imaginary part. Since quantum physics states that a measurement gives a collapse of the wave function to an undetermined state, the measurements, even if they would be made in quick succession, would interfere with each other and energy would be unobservable.


![{\displaystyle [p_{i},q_{j}]\equiv p_{i}q_{j}-q_{j}p_{i}=-i\hbar \delta _{ij},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/da2dc0efd4350fd14a216c592b8cc925b8a9dc4e)








