User talk:Paul Wormer/scratchbook: Difference between revisions
imported>Paul Wormer No edit summary |
imported>Paul Wormer No edit summary |
||
| (40 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
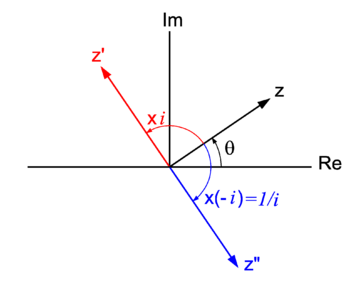
{{Image|Complex number.png|right|350px| Complex number ''z'' ≡ ''r'' exp(''i''θ) multiplied by ''i'' gives <i>z'</i> <nowiki>=</nowiki> <i>z</i>×''i'' | |||
<nowiki>=</nowiki> ''z'' exp(''i'' π/2) (counter clockwise rotation over 90°). Division of ''z'' by ''i'' gives ''z''". Division by ''i'' is multiplication by −''i'' <nowiki> = </nowiki> exp(−''i''  π/2) (clockwise rotation over 90°).}} | |||
==Complex numbers in physics== | |||
===Classical physics=== | |||
Classical physics consists of [[classical mechanics]], [[Maxwell's equations|electromagnetic theory]], and phenomenological [[thermodynamics]]. One can add Einstein's special and general theory of [[relativity]] to this list, although this theory, being formulated in the 20th century, is usually not referred to as "classical". In these four branches of physics the basic quantities and equations governing the behavior of the quantities are real. | |||
physics | |||
Classical mechanics has three different, but equivalent, formulations. The oldest, due to [[Isaac Newton|Newton]], deals with masses and position vectors of particles, which are real, as is time ''t''. The first and second time derivatives of the position vectors enter Newton's equations and these are obviously real, too. The same is true for [[Lagrange formalism|Lagrange's formulation]] of classical mechanics in terms of position vectors and velocities of particles and for [[Hamilton formalism|Hamilton's formulation]] in terms of [[momentum|momenta]] and positions. | |||
[[ | |||
Maxwell equations, that constitute the basis of electromagnetic theory, are in terms of real vector operators ([[gradient]], [[divergence]], and [[curl]]) acting on real [[electric field|electric]] and [[magnetic field|magnetic]] fields. | |||
the | |||
Thermodynamics is concerned with concepts as [[internal energy]], [[entropy]], and [[work]]. Again, these properties are real. | |||
The special theory of relativity is formulated in [[Minkowski space]]. Although this space is sometimes described as a 3-dimensional [[Euclidean space]] to which the axis ''ict'' (''i'' is the imaginary unit, ''c'' is speed of light, ''t'' is time) is added as a fourth dimension, the role of ''i'' is non-essential. The imaginary unit is introduced as a pedestrian way to the computation of the indefinite, real, inner product that in Lorentz coordinates has the metric | |||
:<math> | |||
\begin{pmatrix} | |||
-1 & 0 & 0 & 0 \\ | |||
0 & 1 & 0 & 0 \\ | |||
0 & 0 & 1 & 0 \\ | |||
0 & 0 & 0 & 1 \\ | |||
\end{pmatrix}, | |||
</math> | |||
which obviously is real. In other words, Minkowski space is a space over the real field ℝ. | |||
The general theory of relativity is formulated over real [[differentiable manifold]]s that are locally Lorentzian. Further, the Einstein field equations contain mass distributions that are real. | |||
The | So, although the classical branches of physics do not need complex numbers, this does not mean that these numbers cannot be useful. A very important mathematical technique, especially for those branches of physics where there is flow (of electricity, heat, or mass) is [[Fourier analysis]]. The Fourier series is most conveniently formulated in complex form. Although it would be possible to formulate it in real terms (expansion in terms of sines and cosines) this would be cumbersome, given the fact that the application of the usual trigonometric formulas for the multiplication of sines and cosines is so much more difficult than the corresponding multiplication of complex numbers. Especially electromagnetic theory makes heavy use of complex numbers, but it must be remembered that the final results, that are to be compared with observable quantities, are real. | ||
is | ===Quantum physics=== | ||
a | In quantum physics complex numbers are essential. In the oldest formulation, due to [[Heisenberg]] the imaginary unit appears in an essential way through the canonical commutation relation | ||
:<math> | |||
[p_i,q_j] \equiv p_i q_j - q_j p_i = -i\hbar \delta_{ij}, | |||
</math> | |||
''p''<sub>''i''</sub> and ''q''<sub>''j''</sub> are linear operators (matrices) representing the ''i''th and ''j''th component of the momentum and position of a particle, respectively,. | |||
The time-dependent [[Schrödinger equation]] also contains ''i'' in an essential manner. For a free particle of mass ''m'' the equation reads | |||
:<math> | |||
\frac{\hbar}{2m} \nabla^2 \Psi(\mathbf{r},t) = -i \frac{\partial}{\partial t} \Psi(\mathbf{r},t) . | |||
</math> | |||
This equation may be compared to the [[wave equation]] that appears in several branches of classical physics | |||
:<math> | |||
v^2 \nabla^2 \Psi(\mathbf{r},t) = \frac{\partial^2}{\partial t^2} \Psi(\mathbf{r},t), | |||
</math> | |||
where ''v'' is the [[phase velocity|velocity]] of the wave. It is clear from this similarity why | |||
Schrödinger's equation is sometimes called the wave equation of quantum mechanics. It is also clear that the essential difference between quantum physics and classical physics is the first-order time derivative including the imaginary unit. The classical equation is real and has on the right hand side a second derivative with respect to time. | |||
The more general form of the Schrödinger equation is | |||
:<math> | |||
H \Psi(t) = i \hbar \frac{\partial}{\partial t} \Psi(t) , | |||
</math> | |||
where ''H'' is the operator representing the energy of the quantum system under consideration. If this energy is time-independent (no time-dependent external fields interact with the system), the equation can be separated, and the imaginary unit enters fairly trivially through a so-called phase factor, | |||
:<math> | |||
\Psi(t) = e^{-iEt/\hbar} \Phi\quad\hbox{with}\quad H\Phi = E\Phi. | |||
</math> | |||
The second equation has the form of an operator [[eigenvalue equation]]. The eigenvalue ''E'' (one of the possible observable values of the energy) is real, which is a fairly deep consequence of the quantum laws.<ref>If ''E'' were complex, two separate measurements would be necessary to determine it. One for its real and one for its imaginary part. Since quantum physics states that a measurement gives a collapse of the wave function to an undetermined state, the measurements, even if they would be made in quick succession, would interfere with each other and energy would be unobservable.</ref> The time-independent function Φ can very often be chosen to be real. The exception being the case that ''H'' is not invariant under [[time-reversal]]. Indeed, since the time-reversal operator θ is [[anti-unitary]], it follows that | |||
:<math> | |||
\theta H \theta^\dagger \bar{\Phi} = E \bar{\Phi} | |||
</math> | |||
where the bar indicates [[complex conjugation]]. Now, if ''H'' is invariant, | |||
:<math> | |||
\theta H \theta^\dagger = H \Longrightarrow H\bar{\Phi} = E\bar{\Phi}\quad\hbox{and}\quad | |||
H\Phi = E\Phi, | |||
</math> | |||
then also the real linear combination <math>\Phi+\bar{\Phi}</math> is an eigenfunction belonging to ''E'', which means that the wave function may be chosen real. If ''H'' is not invariant, it usually is transformed into minus itself. Then <math>\Phi\;</math> and <math>\bar{\Phi}</math> belong to ''E'' and −''E'', respectively, so that they are essentially different and cannot be combined to real form. Time-reversal symmetry is usually broken by magnetic fields, which give rise to interactions linear in spin or orbital [[angular momentum]]. | |||
==Note== | ==Note== | ||
<references /> | <references /> | ||
Latest revision as of 09:21, 15 February 2010
Complex numbers in physics
Classical physics
Classical physics consists of classical mechanics, electromagnetic theory, and phenomenological thermodynamics. One can add Einstein's special and general theory of relativity to this list, although this theory, being formulated in the 20th century, is usually not referred to as "classical". In these four branches of physics the basic quantities and equations governing the behavior of the quantities are real.
Classical mechanics has three different, but equivalent, formulations. The oldest, due to Newton, deals with masses and position vectors of particles, which are real, as is time t. The first and second time derivatives of the position vectors enter Newton's equations and these are obviously real, too. The same is true for Lagrange's formulation of classical mechanics in terms of position vectors and velocities of particles and for Hamilton's formulation in terms of momenta and positions.
Maxwell equations, that constitute the basis of electromagnetic theory, are in terms of real vector operators (gradient, divergence, and curl) acting on real electric and magnetic fields.
Thermodynamics is concerned with concepts as internal energy, entropy, and work. Again, these properties are real.
The special theory of relativity is formulated in Minkowski space. Although this space is sometimes described as a 3-dimensional Euclidean space to which the axis ict (i is the imaginary unit, c is speed of light, t is time) is added as a fourth dimension, the role of i is non-essential. The imaginary unit is introduced as a pedestrian way to the computation of the indefinite, real, inner product that in Lorentz coordinates has the metric
which obviously is real. In other words, Minkowski space is a space over the real field ℝ. The general theory of relativity is formulated over real differentiable manifolds that are locally Lorentzian. Further, the Einstein field equations contain mass distributions that are real.
So, although the classical branches of physics do not need complex numbers, this does not mean that these numbers cannot be useful. A very important mathematical technique, especially for those branches of physics where there is flow (of electricity, heat, or mass) is Fourier analysis. The Fourier series is most conveniently formulated in complex form. Although it would be possible to formulate it in real terms (expansion in terms of sines and cosines) this would be cumbersome, given the fact that the application of the usual trigonometric formulas for the multiplication of sines and cosines is so much more difficult than the corresponding multiplication of complex numbers. Especially electromagnetic theory makes heavy use of complex numbers, but it must be remembered that the final results, that are to be compared with observable quantities, are real.
Quantum physics
In quantum physics complex numbers are essential. In the oldest formulation, due to Heisenberg the imaginary unit appears in an essential way through the canonical commutation relation
pi and qj are linear operators (matrices) representing the ith and jth component of the momentum and position of a particle, respectively,.
The time-dependent Schrödinger equation also contains i in an essential manner. For a free particle of mass m the equation reads
This equation may be compared to the wave equation that appears in several branches of classical physics
where v is the velocity of the wave. It is clear from this similarity why Schrödinger's equation is sometimes called the wave equation of quantum mechanics. It is also clear that the essential difference between quantum physics and classical physics is the first-order time derivative including the imaginary unit. The classical equation is real and has on the right hand side a second derivative with respect to time.
The more general form of the Schrödinger equation is
where H is the operator representing the energy of the quantum system under consideration. If this energy is time-independent (no time-dependent external fields interact with the system), the equation can be separated, and the imaginary unit enters fairly trivially through a so-called phase factor,
The second equation has the form of an operator eigenvalue equation. The eigenvalue E (one of the possible observable values of the energy) is real, which is a fairly deep consequence of the quantum laws.[1] The time-independent function Φ can very often be chosen to be real. The exception being the case that H is not invariant under time-reversal. Indeed, since the time-reversal operator θ is anti-unitary, it follows that
where the bar indicates complex conjugation. Now, if H is invariant,
then also the real linear combination is an eigenfunction belonging to E, which means that the wave function may be chosen real. If H is not invariant, it usually is transformed into minus itself. Then and belong to E and −E, respectively, so that they are essentially different and cannot be combined to real form. Time-reversal symmetry is usually broken by magnetic fields, which give rise to interactions linear in spin or orbital angular momentum.
Note
- ↑ If E were complex, two separate measurements would be necessary to determine it. One for its real and one for its imaginary part. Since quantum physics states that a measurement gives a collapse of the wave function to an undetermined state, the measurements, even if they would be made in quick succession, would interfere with each other and energy would be unobservable.

![{\displaystyle [p_{i},q_{j}]\equiv p_{i}q_{j}-q_{j}p_{i}=-i\hbar \delta _{ij},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/da2dc0efd4350fd14a216c592b8cc925b8a9dc4e)








