User:Anthony.Sebastian/SebastianSandbox-2: Difference between revisions
imported>Anthony.Sebastian |
No edit summary |
||
| (55 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
{{AccountNotLive}} | |||
{{TOC|right}} | |||
===article test=== | |||
===ABSTRACT=== | |||
The potential link between dietary sodium chloride (NaCl) intake, hypertension and osteoporosis has been speculated upon for years. Increased NaCl intake is associated with increases in blood pressure in metabolic balance studies as well as in population studies. | |||
Acute NaCl infusions are known to induce a hyperchloremic metabolic acidosis. Accumulating clinical and epidemiologic data suggest that chronic low-grade diet- and age-related metabolic acidosis increase bone resorption and loss of bone mass. | |||
Acute NaCl loading inhibits endothelial nitric oxide synthase in a dose-dependent manner in cell systems and transfected cell lines. Asymmetric dimethylarginine (ADMA) also inhibits the conversion of L-arginine to nitric oxide. Nitric oxide (NO) is a direct vasodilator, and decreases in NO production are associated with higher blood pressures. | |||
Subjects who are particularly sensitive to salt, defined as an increase in mean arterial pressure (MAP) of at least 5 mmHg after an increase in dietary salt intake from 30 to 250 mmol/day, have increased levels of ADMA, resulting in less nitric oxide production, leading to higher blood pressures. In addition, on high salt diets, salt sensitive subjects have increased urinary calcium excretion compared to salt resistant subjects. | |||
Those considerations raise the possibility that salt sensitivity is the key to predicting who, on a high NaCl diet, would be particularly prone to developing not only high blood pressure, but increased bone breakdown which can predispose to osteoporosis. | |||
===NaCl, METABOLIC ACIDOSIS AND BONE=== | |||
Metabolic acidosis in i''n vitro'' studies induces increased osteoclast activation and bone resorption, decreased osteoblast activation and bone mineralization and increased calcium loss from bone as the systemic pH decreases,</sup>.. Bushinsky et al. have elegantly demonstrated in mouse calvarie that urine calcium efflux from bone dose-dependently increases as the systemic pH and plasma bicarbonate concentration decrease, whether the bone cells are alive, dead or stimulated with PTH or vitamin D. This group has also recently shown that OGR-1 is the proton sensing receptor on the ''osteoblasts ''that induces activation of the ''osteoclasts ''in a high acid environment. | |||
Cross-sectional analyses of human metabolic balance studies demonstrate that increased ingestion of dietary NaCl is independently associated with lower steady-state blood pH (increased acid levels) and lower steady-state plasma bicarbonate levels within the range considered to be normal, (viz. a low grade chronic metabolic acidosis) compared with ingestion of a lower dietary NaCl intake. This effect is independent of the diet net acid load, renal function and the partial pressure of carbon dioxide, the three other variables that have been shown to regulate systemic pH and bicarbonate. | |||
The dose-dependent effects of NaCl on acid production and excretion are even more pronounced in salt-sensitive rats. Batlle et al. demonstrated in Dahl/Rapp salt sensitive and salt resistant rats not only that urine net acid excretion (NAE) increased as NaCl intake increased, but that the NAE increases in the salt sensitive rats was significantly greater than in the salt resistant rats ''at all levels of salt intake. ''In other words, the salt sensitive rats had more of a metabolic acidosis with any salt intake than the salt resistant rats. | |||
More recently, a small prospective study in young healthy subjects has demonstrated that dietary NaCl increases this low grade chronic metabolic acidosis in a dose-dependent fashion and this is associated with significant dose dependent increases in urinary excretion of calcium and of bone resorption markers such as C-telopeptide. Sharma et al. has also shown that salt sensitive humans had significantly lower blood pH and plasma bicarbonate levels on high salt diets compared to salt resistant subjects. Whether salt sensitive subjects also have greater urinary calcium or bone breakdown marker concentrations would be predicted, but has not been demonstrated. | |||
'''NaCl AND NITRIC OXIDE SYNTHESIS''' | |||
Nitric oxide (NO) is generated from L-arginine by the enzyme nitric oxide synthase. In vascular endothelial cells, nitric oxide is a direct vasodilator, leading to decreased blood pressure. Recently, NaCl has also been shown to dose-dependently decrease endogenous nitric oxide synthase (eNOS) activity in both bovine aortic endothelial cells (BAEC) as well as transfected Chinese hamster ovarian cells (CHO-eNOS). <nowiki>This effect seems to be mediated by the sodium ion, as NaPO4 [comment: PO4 trivalent, so formula would read Na3PO4, unless H2PO4 intended, in which case NaH2PO4 would yield acidic medium, I think.] also dose-dependently decreased eNOS activity. </nowiki> | |||
Asymmetric dimethylarginine (ADMA), which derives from the methylation of arginine residues in proteins, is a competitive inhibitor of eNOS, and increases in ADMA inhibit nitric oxide related vasodilation, leading to increased blood pressure. In 13 salt sensitive normotensive subjects, Fang el al. demonstrated significantly higher mean blood pressures and ADMA levels on a high salt diet, compared to a low salt diet and compared to 47 salt resistant subjects on either salt diet. | |||
'''NITRIC OXIDE AND BONE''' | |||
Interestingly, several recent clinical studies have suggested that giving nitrates <nowiki>[explain relation of nitrates and nitric oxide] will improve bone mineral density.</nowiki>, </sup><nowiki>A recent comparison study by Nabhan and Rabie demonstrated in 60 postmenopausal women with osteoporosis that 12 months treatment with isosorbide dinitrate 20 mg daily was as effective as alendronate 70 mg weekly in improving bone mineral density (BMD) and DEXA T-score (10.8% vs. 12.1% respectively; p<0.05 for each within group increase, p=0.7 for between group differences). </nowiki> | |||
Nitric oxide synthases have been demonstrated in both osteoclasts and osteoblasts. Rats that are deficient for the eNOS gene have significant reduction in bone formation. Nitric oxide produced by bone cells may play an important role in mechanical-strain induced bone remodeling.. | |||
Nitric oxide may also be the mediator by which estrogen or androgen therapy improves BMD. Studies in castrated or oophorectomized rats given the NOS blocker L‑NAME demonstrated no loss of the usual sex-steroid-deficiency-induced BMD compared to the rats not given L-NAME.<nowiki> [do not follow this reasoning]</nowiki> | |||
'''SALT SENSITIVITY AND BONE METABOLISM''' | |||
From the previous paragraphs, dietary NaCl would be expected to affect bone metabolism in two ways; by inducing a low grade metabolic acidosis and by inhibiting nitric oxide production. The data also suggests that these effects will be seen especially in those subjects who are salt sensitive. Schmidlin et al. studied the effects of NaCl intake in 47 salt-sensitive (SS) and salt-resistant (SR) normotensive subjects on blood pressure, ADMA production and urine calcium excretion on both a low (30 mmol/day) salt and a high (250 mmol/day) diet in a 2 week crossover metabolic balance study. As expected, NaCl loading induced a significant increase in mean arterial pressure (MAP) in the SS but not in the SR subjects, associated in increases in ADMA only in the SS group, p=0.007. ADMA levels were significantly correlated with urine calcium excretion only in the salt sensitive group (R<sup>2</sup><nowiki>=0.47, p=0.02), with no correlation in the SR group (R</nowiki><sup>2</sup><nowiki>=0.03, p=0.57).</nowiki> Urine pH?…. | |||
Studies suggest that subjects with risk factors for metabolic syndrome are also more likely to be salt sensitive. Chen et al. studied 1881 subjects in northern China and evaluated them for salt sensitivity as well as the presence of markers for the metabolic syndrome; dyslipidemia, abdominal obesity, hyperglycemia and elevated blood pressure. After adjustment for age, sex, education, physical activity, cigarette smoking, body mass index and 24-hour urinary sodium and potassium excretion, there was a progressive increase in the relative risk for salt sensitivity as the number of risk factors for metabolic syndrome increased (four or five factors; OR 3.54, CI 2.05-6.11). Metabolic syndrome has been associated with lower urine pH values and lower nitric oxide levels.<nowiki> [relevance to osteoporosis? </nowiki>No mention of bone.] | |||
Conversely, subjects who are insensitive to salt, such as those with mutations leading to renal salt wasting, might be expected to have less salt-induced bone resorption. Cruz et al. has shown that subjects who are homozygous for the NCCT mutation (of the thiazide sensitive Na-Cl transporter in the distal tubule in the kidney) have significantly higher serum bicarbonate levels, lower urine calcium excretion associated with higher urine Na excretion, and higher BMDs than subjects who are heterozygous for the mutation, and both groups are higher than subjects who are homozygous for the wild-type alleles. | |||
'''COMMON FINAL PATHWAY?''' | |||
Is there a relationship between metabolic acidosis and nitric oxide synthesis? Studies by Mitch et al. over the last decade have demonstrated that in muscle cells metabolic acidosis inhibits the signaling pathway for insulin and IGF-1, leading to decreased intracellular phosphoinositol-3-kinase (PI3K) activity, which in turn leads to activation of nuclear factors, caspase-3 activity and increased protein degradation. In endothelial cells, IGF-1 is the receptor that activates PI3K leading to increased nitric oxide synthesis. | |||
NaCl, then, might in fact have a “double whammy†effect on bone; 1) by inducing a metabolic acidosis and 2) by inhibiting NO production, the latter resulting perhaps separately from metabolic acidosis (inhibiting IGF-1 signalling) and from salt loading (enhancing ADMA levels). Those subjects who are particularly sensitive to the effects of NaCl would be those subjects most likely to demonstrate increased bone breakdown and decreased BMD. This hypothesis would help solidify the previously speculated upon but unproven relationship between hypertension and osteoporosis, and perhaps other metabolic disease, such as diabetes and metabolic syndrome, and osteoporosis. | |||
'''CONCLUSIONS''' | |||
To review the points that have been covered in this manuscript: | |||
# NaCl intake dose-dependently induces increased degrees of metabolic acidosis and high blood pressure, independently of known acidosis-producing factors; | |||
# NaCl stimulates ADMA, which reduces NO levels, and correlates with higher blood pressure in all subjects; and, in SS subjects increases urinary calcium excretion, the latter potentially due to increased net bone resorption. | |||
# Thus, in SS subjects increased NaCl intake induces a metabolic acidosis and reduces NO synthesis, a “DOUBLE JEOPARDY†resulting in pressor and osteoporotic effects. | |||
<nowiki>[summary should expand to cover all the main pathophysiological connections discussed in paper.]</nowiki> | |||
<nowiki>[Very original and sophisticated synthesis – think NIH grant, NaCl reduction to eliminate two big killers of elderly, or KBC to counteract the effect of NaCl, as a natriuretic and chlouretic, and as an acid neutralizer.]</nowiki> | |||
==dalton image== | |||
{{Image|JOHN DALTON REICH-CHEMMISTRY.jpg|right|350px|'''Portrait of John Dalton.''' Courtesty [https://reich-chemistry.wikispaces.com/Fall.2008.MMA.LeClerc.Timeline Reich-Chemistry Wikispaces.][http://www.creativecommons.org/licenses/by-sa/3.0 Creative Commons Attribution Share-Alike 3.0 License.]}} | |||
==Mole (Chemistry)== | |||
Chemists employ standard units of measurement to characterize samples of the substances they study. For example: | |||
*they use the basic unit designated ''liter'' (abbr., L) to characterize the volume of the sample, viz., the amount of three-dimensional space the sample occupies. Under the same conditions, 1.45 L of water occupies the same volume as 1.45 L of ethanol (drinking alcohol). | |||
*they use the basic unit designated ''kilogram'' (abbr., kg) to characterize the ''mass'' of the sample, viz., the quantity of matter in the sample as reflecting the force required to accelerate it (force equals mass times acceleration, F=ma). 1.52 kg of water contains the same mass of matter as 1.52 kg of ethanol. | |||
Often chemists want to characterize a sample of a substance by a unit of measurement that represents the number of molecules the sample contains. Here we will discuss that unit in relation to pure substances, e.g., those that contain only one type of molecule, as in the case of samples of pure water, pure glucose, pure dioxygen, etc. — namely, chemical compounds. | |||
For the purpose, chemists invented the basic unit designated '''mole'''. Just as equal liters of different chemical compounds occupy the same volume, and equal masses of different chemical compounds contain the same quantity of matter, equal moles of different chemical compounds contain the same number of molecules. | |||
Without a deep understanding of the concept and application of the mole, one cannot exploit chemistry to develop understanding biology and medicine, or to produce industrial and technological advances. | |||
In this article, we will describe how chemists define the unit, mole, in a way that allows it to reflect the number of molecules in a sample of a chemical compound; how they determine the number of moles in a sample; how they use the unit to characterize chemical reactions and for many other purposes; and how they extend use of the unit to samples of chemical elements and of other types of pure chemical substances besides compounds and elements | |||
===Creeping up on moles=== | |||
==== What do we need to know to understand the concept of mole?==== | |||
*the definition of mass | |||
*the standard units of mass, including the units of mass of atoms | |||
*the definitions of molecule and chemical compound | |||
*the masses of the atoms of the elements | |||
*what an isotope means | |||
*the relative abundances of the various isotopes of an element | |||
*how to calculate the number of molecules in a sample of a chemical compound | |||
=== The mass of single atoms of the chemical elements=== | |||
A ''molecule'' of a chemical compound consists of two or more different types of atoms (e.g., hydrogen and oxygen atoms when considering a water molecule) bound together in a fixed ratio per molecule (e.g., two hydrogen atoms to one oxygen atom per molecule of water). To understand how the unit of measurement, mole, gives a representation of the number of molecules in a sample of a chemical compound (e.g., 1.0 L of water; 1.0 kg of dioxygen gas), we first need to know the masses of the atoms that make up the sample.<ref><font color="purple"><u>'''Note:'''</u></font> This discussion requires accepting the standard units of mass, including atomic mass, as established by international agreement.</ref> Each of the 92 different types of atoms (making up the 92 naturally-occurring elements) has a different 'mass number', referred to as the ''atomic mass number''. Moreover, the atoms of many elements exist as multiple 'isotopes' that have differing number of neutrons, hence in atomic mass number, accompanying their element-unique number of protons and electrons. | |||
=== Using atomic mass numbers to calculate the number of molecules in samples of chemical compounds=== | |||
If we knew the mass numbers of the different types of atoms in a chemical compound, <ref><font color="purple"><u>'''Note:'''</u></font> Chemists have devised methods for determining the masses of atoms (e.g., mass spectroscopy) and have compiled lists of the mass numbers of the various isotopes of the naturally-occurring elements.</ref> | |||
the relative abundance and mass numbers of the several isotopes of those element’s atoms, the ratio of the different types of atoms making up the molecules of the chemical compound, and the total mass of the sample of the chemical compound, we could, with simple algebra, calculate the number of molecules in the sample. | |||
Consider 1.0 g (1/1000th of a kg) of water, each molecule of which consists of two hydrogen atoms and one oxygen atom. Almost all hydrogen atoms exist as the isotope that has one proton and one electron (no extra neutrons), each atom with a mass of 1.674 x 10<sup>-21</sup> kg, or 1.674 x 10<sup>-24</sup> g, where one g equals 1/1000th of a kg (=10<sup>-3</sup> kg). Almost all oxygen atoms exist as the isotope that has eight protons, eight neutrons, and eight electrons, designated O-16, each atom with a mass of 2.655 x 10<sup>-23</sup> g. ''Ignoring the minor isotopes'', and considering that water consists of two hydrogen atoms and one oxygen atom per molecule, we calculate the mass of a molecule of water as 2 x 1.674 x 10<sup>-24</sup> + 2.655 x 10<sup>-23</sup>, or 2.990 x 10<sup>-23</sup> g/molecule. 1.0 g of water then must contain (1.0 g /2.990 x 10<sup>-23</sup> g/molecule), or 3.34 x 10<sup>22</sup> molecules. | |||
=== Scaling up atomic mass numbers for convenience: the 'atomic mass unit'=== | |||
From the previous section we can conclude that a fifth of a teaspoon of water (~1.0 g) contains about 300 billion times more molecules than the number of stars in our galaxy, a consequence of the minute masses of its atoms. In fact, for all elements, atomic mass numbers range from about 10<sup-24</sup> to 10<sup-22</sup> g, all very minute. For convenience, chemists minimize dealing with such small numbers by defining a unit that serves as a marker, or conversion factor, for the atomic mass numbers. They call it the “atomic mass unit” (abbr., amu), and define it as 1/12 of the mass of one atom of the most abundant isotope of carbon, carbon-12 (6 protons, 6 neutrons, six electrons), the latter equal to 1.9926 x 10<sup>-23</sup> g, 1/12th of which equals 1.6605 x 10<sup>-24</sup> g. Thus, | |||
<center>1 amu = 1.6605 x 10<sup>-24</sup> g.</center> | |||
Using that formula as a conversion factor, one can compute how many atomic mass units (amu’s) for any atom, knowing the atom’s mass number. O-16, with a mass number as mentioned of 2.655 x 10<sup>-23</sup> g, must have [(2.655 x 10<sup>-23</sup> g/atom)/1.6605<sup>-24</sup> g/amu)] amu, or 15.99 amu. Thus, an oxygen atom has a mass of 15.99, expressed as atomic mass units. Knowing the conversion formula, we can always get back to oxygen’s mass in grams. | |||
Converting atomic mass numbers to atomic mass units still allows us to determine the number of molecules in a sample of a chemical compound. We use the same procedure as we employed using atomic mass numbers, except now we use the more convenient small numbers of atomic mass units. | |||
=== The minor isotopes: a little more chemistry before we can grasp the mole=== | |||
Ignoring the minor isotopes of the atoms in the molecule of a chemical substance, as we did in the earlier example of calculating the number of molecules in a sample of a chemical compund, will not allow us to ''accurately'' calculate the number of molecules in the sample. Without incorporating them, we will not know the ''average'' atomic mass of a given atom type that has isotopes with slightly differing atomic mass units. To incorporate all of an element’s isotopes in getting the element’s atoms’ ''average'' atomic mass we must know the atomic mass units of each isotope, as well as its relative abundance among all the isotopes of the element. With a little algebra, we can then calculate the average mass of the atoms of a given element, and express the results in atomic mass units, for convenience. | |||
Logically we would call the result the atomic mass of the element’s atoms, averaged out for all of the element’s isotopes. However, by tradition chemists call the result the ''atomic weight (AW)'' of the element’s atoms, the number we find in the periodic table. | |||
For a simple example of how to calculate the atomic weight of an element, consider the element, oxygen. Oxygen has three naturally occurring isotopes of its atoms: O-16, amu=15.99491463, abundance=99.757%; O-17, amu=16.9991312, abundance=0.038%; O-18, amu=17.9991603, abundance=0.205%. We can calculate how much each isotope contributes the mass of the element’s atoms by the product of its fractional abundance and its atomic mass expressed in atomic mass units. By adding together those products we then get atomic mass of the element’s atoms averaged among the several isotopes, as if all the atoms had the same atomic mass. For oxygen, the calculation can be written as: | |||
<center>Atomic weight (AW) = [(99.75/100)*15.99491463] + [(0.038/100)*16.9991312] + [(0.205/100)*17.9991603] = 15.9994 atomic mass units (amu)</center> | |||
We see that number as the atomic weight of oxygen in the periodic table. | |||
===Grasping the mole=== | |||
We now have nearly all we need to grasp the concept of mole. We just need a formal definition of mole. In defining the mole, chemists have done something similar to defining atomic mass units: they devised a definition that allow expressing large numbers (e.g., 10<sup>20</sup>) of molecules in convenient small numbers. | |||
Without background of history or rationale at this point, we give the formal definition of mole: | |||
'''One mole''' (of any chemical compound, say) equals the number of atoms in exactly 12 g of the major isotope of carbon, carbon-12. | |||
:*That definition tells us immediately that one mole of every chemical compound has the same number of molecules as the number of atoms in one mole, or 12 g, of carbon-12. | |||
Just how many atoms does one mole, or 12 g, of cabon-12 have? We showed in an earlier section how to calculate the number of molecules in a given sample of a chemical compound. We can use the same method for determining how many atoms in a given sample, 12 g, of carbon-12. | |||
:*First we obtain from an appropriate look-up table the mass (i.e., atomic mass number) of one atom of carbon-12. We obtain 1.9926 x 10<sup>-23</sup> g/ carbon-12 atom. | |||
:*Our sample contains 12 g carbon-12 atoms. | |||
:*For 12 g carbon-12, and 1.9926*10<su>-23</sup> g per carbon-12 atom, with grams cancelling out, we can write: | |||
::*12 g carbon-12/1.9226*10<sup>-23</sup> g/carbon-12 atom = 6.022*10<sup>23</sup> carbon-12 atoms | |||
Thus, 12 g carbon-12 contains 6.022*10<sup>23</sup> atoms. | |||
Since the number of atoms in 12 g carbon-12 by definition equals one mole of carbon-12, and one mole of any chemical compound has the same number of molecules as does one mole of carbon-12, ''one mole of any chemical compound contains 6.022*10<sup>23</sup> molecules.'' | |||
Although chemists define the mole in terms of carbon atoms, the mole unit (6.022*10<sup>23</sup> carbon atoms) applies to any sample of a pure substance (chemical compounds, atoms, ion, electrons, quanta, etc.) — each of which contains 6.022*10<sup>23</sup> of its constituents, just as one score means 20 of any item (see Gettysburg Address) and one dozen means 12 of any item. In the chemistry of pure substances one mole means 6.022*10<sup>23</sup> of any constituent. | |||
If we remember that we can interconvert atomic mass numbers, ranging from 10<sup>-22</sup> to 10<sup>-24</sup> g, to atomic mass units (amu’s), ranging more conveniently from ~1 to ~240 amu, we can also use amu’s to calculate the number of items in one mole. | |||
:*One amu = 1/12th of the atomic mass number of one carbon-12 atom, the latter equal to 1.9926*10<sup>-23</sup>, 1/12th of which equals 1.6605*10<sup>-24</sup> g (viz., .9926*10<sup>-23</sup> g/12). | |||
:*Since one amu is 1/12th the atomic mass number of one carbon-12 atom, that means one carbon-12 atom has a mass in amu’s 12 times that, or precisely 12 amu. | |||
:*The number of atoms in a sample of 12 g carbon-12 then computes as: | |||
<center>12 g carbon-12 atoms/12 amu</center> | |||
<center>or</center> | |||
<center>12 g carbon-12 atoms/12*1.6605*10<sup>-24</sup> g = 6.022*10<sup>23</sup> carbon-12 atoms</center> | |||
Again, then 12 g carbon-12, or one mole of carbon-12, has 6.022*10<sup>23</sup> atoms. | |||
===Chemists call the number of constituent items in one mole of an element or chemical compound Avogadro’s number=== | |||
To repeat, 1 mole of atoms of every element equals 6.022*10<sup>23</sup> atoms, and one mole of a sample of any pure substance (molecules, ions, electrons, radicals, quanta, etc.) likewise contains 6.022*10<sup>23</sup> of its constituent items. | |||
Chemists refer the number 6.022*10<sup>23</sup> as ''Avogadro’s Number (N<sub>A</sub>)'', after the pioneering physicist, [[Amedeo Avogadro|Amedeo Avogadro]] (1776-1856), who first recognized the distinction between atoms and molecules. To get a sense of the size of Avogadro’s number, the Oxford chemist, Peter Atkins called attention to the visualization that with an Avogadro’s number, one mole, of soft-drink cans one could cover the surface of the earth with a pile 200 miles high. | |||
====Use this from SI Brochure==== | |||
SI brochure, Section 2.1.1.6 | |||
Following the discovery of the fundamental laws of chemistry, units called, for example, "gram-atom" and "gram-molecule", were used to specify amounts of chemical elements or compounds. These units had a direct connection with "atomic weights" and "molecular weights", which are in fact relative masses. "Atomic weights" were originally referred to the atomic weight of oxygen, by general agreement taken as 16. But whereas physicists separated the isotopes in a mass spectrometer and attributed the value 16 to one of the isotopes of oxygen, chemists attributed the same value to the (slightly variable) mixture of isotopes 16, 17 and 18, which was for them the naturally occurring element oxygen. Finally an agreement between the International Union of Pure and Applied Physics (IUPAP) and the International Union of Pure and Applied Chemistry (IUPAC) brought this duality to an end in 1959/60. Physicists and chemists have ever since agreed to assign the value 12, exactly, to the so-called atomic weight of the isotope of carbon with mass number 12 (carbon 12, 12C), correctly called the relative atomic mass Ar(12C). The unified scale thus obtained gives the relative atomic and molecular masses, also known as the atomic and molecular weights, respectively. | |||
The quantity used by chemists to specify the amount of chemical elements or compounds is now called "amount of substance". Amount of substance is defined to be proportional to the number of specified elementary entities in a sample, the proportionality constant being a universal constant which is the same for all samples. The unit of amount of substance is called the mole, symbol mol, and the mole is defined by specifying the mass of carbon 12 that constitutes one mole of carbon 12 atoms. By international agreement this was fixed at 0.012 kg, i.e. 12 g. | |||
Following proposals by the IUPAP, the IUPAC, and the ISO, the CIPM gave a definition of the mole in 1967 and confirmed it in 1969. This was adopted by the 14th CGPM (1971, Resolution 3): | |||
1. The mole is the amount of substance of a system which contains as many elementary entities as there are atoms in 0.012 kilogram of carbon 12; its symbol is "mol". | |||
2. When the mole is used, the elementary entities must be specified and may be atoms, molecules, ions, electrons, other particles, or specified groups of such particles. | |||
It follows that the molar mass of carbon 12 is exactly 12 grams per mole, M(12C) = 12 g/mol. | |||
In 1980 the CIPM approved the report of the CCU (1980) which specified that | |||
In this definition, it is understood that unbound atoms of carbon 12, at rest and in their ground state, are referred to. | |||
The definition of the mole also determines the value of the universal constant that relates the number of entities to amount of substance for any sample. This constant is called the Avogadro constant, symbol NA or L. If N(X) denotes the number of entities X in a specified sample, and if n(X) denotes the amount of substance of entities X in the same sample, the relation is | |||
n(X) = N(X)/NA. | |||
Note that since N(X) is dimensionless, and n(X) has the SI unit mole, the Avogadro constant has the coherent SI unit reciprocal mole. | |||
In the name "amount of substance", the words "of substance" could for simplicity be replaced by words to specify the substance concerned in any particular application, so that one may, for example, talk of "amount of hydrogen chloride, HCl", or "amount of benzene, C6H6". It is important to always give a precise specification of the entity involved (as emphasized in the second sentence of the definition of the mole); this should preferably be done by giving the empirical chemical formula of the material involved. Although the word "amount" has a more general dictionary definition, this abbreviation of the full name "amount of substance" may be used for brevity. This also applies to derived quantities such as "amount of substance concentration", which may simply be called "amount concentration". However, in the field of clinical chemistry the name "amount of substance concentration" is generally abbreviated to "substance concentration". | |||
http://www.bipm.org/en/si/si_brochure/chapter2/2-1/mole.html | |||
The 11th General Conference on Weights and Measures (1960) adopted the name Système International d'Unités (International System of Units, international abbreviation SI), for the recommended practical system of units of measurement. | |||
The 11th CGPM laid down rules for the prefixes, the derived units, and other matters. The base units are a choice of seven well-defined units which by convention are regarded as dimensionally independent: the metre, the kilogram, the second, the ampere, the kelvin, the mole, and the candela. Derived units are those formed by combining base units according to the algebraic relations linking the corresponding quantities. The names and symbols of some of the units thus formed can be replaced by special names and symbols which can themselves be used to form expressions and symbols of other derived units. | |||
The SI is not static but evolves to match the world's increasingly demanding requirements for measurement. | |||
The International System of Units (SI) | |||
==See also== | |||
:* [http://www.answers.com/topic/mole several sources, incl. hx] | |||
:* Wichers 1962<ref name=wichers1962>Wichers E. (1962) [http://dx.doi.org/10.1038/194621a0 New Scale of nuclidic masses and atomic weights.] ''Nature'' 194:621-624.</ref> | |||
==References [mole]== | |||
<references/> | |||
==test== | |||
[[Image:Longevity disparities.JPG|right|thumb|400px|{{A-image|U.S. Department of Health and Services; Data from U.S. Department of Health and Human Services, synthesized by Singh GK, Siahpush M. (2006) [http://dx.doi.org/10.1093/ije/dyl083 Widening socioeconomic inequalities in US life expectancy, 1980–2000. (Free Full-Text)] Int. J. Epidemiol. Advance Access Publication; Chart from data in Singh and Siahpush’s report by the New York Times, March 23, 2008.<br/>|}}Widening socioeconomic inequalities in life expectancy among Americans during 1980 to 2000.]] | |||
xxx<ref name=ilberg1927>Ilberg J. (1927) [http://www.jstor.org/pss/693804 Sorani Gynaeciorum Libri N. De signis fracturarum.] De fascUs. Vita Hippocratis secundum Soranum (CMG IV), Leipzig & Berlin.</ref> | |||
When someone writes history, we call that person a historian. When a historian of fervent curiosity bases the writing of history in particular on critical analysis of historical source material and provides a narrative synthesis that receives the approprobation of critical analysis, we may refer to the person more technically, and with more distinction, as a '''historiographer''' (etymologically a grapher of what one has learned through inquiry). We refer to the historiographer's writing of history as '''historiography''' — i.e., the historiographer's art or occupation. Thus, [[Herodotus]], the Greek historian whose life nearly spanned the 5th century BCE, and whom the Roman scholar, [[Cicero]] (106-43 BCE), dubbed 'the father of history', occupied himself with the 'art' of historiography, writing of the wars of the Greeks and Persians — in the process setting a precedent for historiographers to come. | |||
The term historioigraphy may apply, in another sense, to the ''study'' of historical writing, to the history of historical writing, and to the theoretical bases of historical writing, in contrast to the study of the history per se. The journal [http://www.dur.ac.uk/Classics/histos/ ''Histos'' ("''The Electronic journal of ancient historiography at the university of Durham.''")] states that its ''....focus will be more on the historical texts and media than on the historical problems for which those texts and media are sources, though the emphasis may naturally vary.'' For example, see the article by Clemence Schultze, entitled "Authority, originality and competence in the ''Roman Archaeology'' of Dionysius of Halicarnassus".<ref>Schultze C. (2000) [http://www.dur.ac.uk/Classics/histos/2000/schultze1.html Authority, originality and competence in the ''Roman Archaeology'' of Dionysius of Halicarnassus.] ''Histos'' Vol. 4, December | |||
*'''<u>Opening paragraph:</u>''' Any attempt to understand an ancient historian’s programme, claim to authority, self-definition,[citation] originality and ideas about history and historiography must begin with analysis of his prefatory statements.[citation] Dionysius’ preface (whose literary and intellectual quality has generally been underestimated) reveals how his authority rests at once upon his predecessors and upon himself. At the very outset, in a single long and impressive sentence, he marks his knowledge of, and simultaneously his distance from, those predecessors; he expresses his attitude to his role and his materials; and he asserts the logismoi (‘reasonings’) and empeiria (‘knowledge’) which underpin his work: [Dionysius's sentence follows]</ref> | |||
Thus, a historiographer may write history or study how historiographers write history. | |||
<references /> | |||
==refs== | |||
<references /> | |||
==Image test== | |||
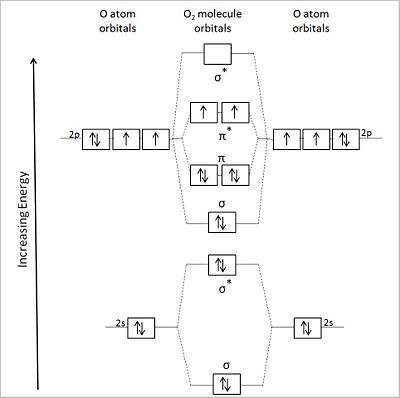
[[Image:Oxygen molecule orbitals diagram.JPG||right|thumb|400px|{{#ifexist:Template:Oxygen molecule orbitals diagram.JPG/credit|{{Oxygen molecule orbitals diagram.JPG/credit}}<br/>|}}Diagrammatic representation of the molecular orbitals of an oxygen molecule (center) formed by the overlapping valence shell orbitals of two flanking oxygen atoms (left and right of center. Asterisks designate antibonding orbitals.]] | |||
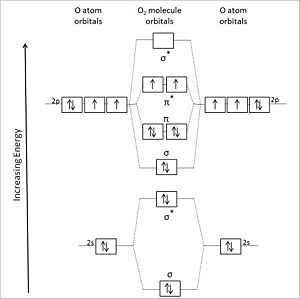
[[Image:Oxygen molecule orbitals diagram.JPG||right|thumb|300px|{{#ifexist:Template:Oxygen molecule orbitals diagram.JPG/credit|{{Oxygen molecule orbitals diagram.JPG/credit}}<br/>|}}Diagrammatic representation of the molecular orbitals of an oxygen molecule (center) formed by the overlapping valence shell orbitals of two flanking oxygen atoms (left and right of center. Asterisks designate antibonding orbitals.]] | |||
==Risks of Developing Osteoporosis in Women and Men== | |||
Fractures, a common consequence of osteoporosis, and often the first indication of the disease, rank as osteoporosis' most adverse consequence. It of causes severe pain and debilitation, especially in the elderly who fall and fracture their hip, and it can lead to death from complications during the planned recovery period. Some 20% of hip fracture patients die within a year (Leibson et al. 2002). | |||
:<blockquote>The 1.5 million osteoporotic fractures in the United States each year lead to more than half a million hospitalizations, over 800,000 emergency room encounters, more than 2,600,000 physician office visits, and the placement of nearly 180,000 individuals into nursing homes. Hip fractures are by far the most devastating type of fracture, accounting for about 300,000 hospitalizations each year (Surgeon General 2004).</blockquote> | |||
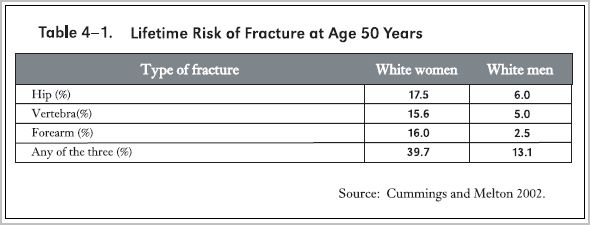
The accompanying table from the Surgeon General's 2004 report (Surgeon General 2004) indicates that at age 50 years white women carry a lifetime risk of hip, spine or forearm fracture amounting to nearly 40%, and men about 13%. | |||
{{Image|Fig lifetime ris fx SG Report.JPG|center|800px|Surgeon General Report on Bone Health and Osteoporosis in 2004 (Surgeon General 2004).}} | |||
The gender difference relates ''in part'' to the faster waning of sex steroid hormones in women as they age, menopause predating the more gradual andropause. Male and female sex hormones act on bone in a positive way, not surprisingly since successful reproduction depends in many ways on healthy bones in the parents. | |||
==References Cited== | |||
::''Listed here in alphabetical order by last name of first author as cited with publication date in the text.'' | |||
*'''Leibson CL, Tosteson AN, Gabriel SE, Ransom JE, Melton LJ. (2002) Mortality, disability, and nursing home use for persons with and without hip fracture: a population-based study. J Am Geriatr. Soc. 50(10):1644-50. PMID 12366617.''' | |||
::*'''<u>Abstract:</u>''' OBJECTIVES: To compare persons with and without hip fracture for subsequent mortality and change in disability and nursing home (NH) use. DESIGN: Population-based historical cohort study. SETTING: Olmsted County, Minnesota. PARTICIPANTS: All residents who experienced a first hip fracture between January 1, 1989, and December 31, 1993, and, for each case, a resident of the same sex and similar age who had not experienced a hip fracture and was seen by a local care provider. MEASUREMENTS: Data on disability (Rankin score), comorbidity (Charlson Index), and NH residency before baseline (fracture date for cases and registration date for controls) were obtained by review of complete community-based medical records. The records were then reviewed from baseline through December 31, 1994, for Rankin disability at 1 month and 1 year, all NH admissions and discharges, and date of death for those who died. RESULTS: There were 312 cases and 312 controls (81% female, mean age +/- standard deviation = 81 +/- 12 years). Before baseline, cases had higher comorbidity (45% vs 30% had Charlson Index >/= 1, P <.001) and disability (mean Rankin score = 2.5 +/- 1.1 vs 2.2 +/- 1.1, P <.001) and were more likely to be in a NH (28% vs 18%, P <.001) than controls. One year after baseline, estimated mortality was 20% (95% confidence interval (CI) = 16-24) for cases vs 11% (95% CI = 8-15) for controls, 51% of cases versus 16% of controls had a level of disability one or more units worse than before baseline (P <.001), and the cumulative incidence of first NH admission was 64% (95% CI = 58-71) for cases versus 7% (95% CI = 4-11) for controls. The risk of NH admission for cases relative to controls diminished over time, but remained elevated 5 years after the event (risk ratio = 20.0 at 3 months and 2.1 at 5 years), but, in persons admitted to a nursing home, cases were two times more likely than controls to be discharged alive within a year (P <.001). CONCLUSIONS: Hip fracture is an important contributor to disability and NH use, but the potential savings from hip fracture prophylaxis may be overestimated by studies that fail to consider differential risk, mortality, and long-term follow-up. | |||
*'''Cummings SR, Melton LJ. (2002) Epidemiology and outcomes of osteoporotic fractures. Lancet 359(9319):1761-7 PMID 12049882.''' | |||
::*'''<u>Abstract:</u>''' Bone mass declines and the risk of fractures increases as people age, especially as women pass through the menopause. Hip fractures, the most serious outcome of osteoporosis, are becoming more frequent than before because the world's population is ageing and because the frequency of hip fractures is increasing by 1-3% per year in most areas of the world. Rates of hip fracture vary more widely from region to region than does the prevalence of vertebral fractures. Low bone density and previous fractures are risk factors for almost all types of fracture, but each type of fracture also has its own unique risk factors. Prevention of fractures with drugs could potentially be as expensive as medical treatment of fractures. Therefore, epidemiological research should be done and used to identify individuals at high-risk of disabling fractures, thereby allowing careful allocation of expensive treatments to individuals most in need. | |||
*'''Surgeon General Report. (2004) [http://www.surgeongeneral.gov/library/bonehealth/ Bone Health and Osteoporosis]''' | |||
==Notes (numbered as footnotes in text)== | |||
<references /> | |||
---- | |||
---- | |||
==Scientists== | ==Scientists== | ||
For biographies of scientists. | For biographies of scientists. | ||
| Line 18: | Line 328: | ||
==Table from OO== | ==Table from OO== | ||
{|align=center width=70%; | |||
| | |||
{| class="prettytable" | {| class="prettytable" | ||
| <center>'''DATE'''</center> | | <center>'''DATE'''</center> | ||
| <center>''' | | <center>'''EVENTS PERTINENT TO THE LIFE, WORK AND TIMES OF J.B.S. HALDANE'''</center> | ||
|- | |- | ||
| Line 30: | Line 341: | ||
| <center>'''1837-1901'''</center> | | <center>'''1837-1901'''</center> | ||
| The Victorian Age: Reign of Victoria, Queen of England and Ireland | | The Victorian Age: Reign of Victoria, Queen of England and Ireland | ||
|- | |||
| <center>'''1859'''</center> | |||
| Charles Darwin publishes ''On the Origin of Species, or the Preservation of Favoured Races in the Struggle for Survival''. | |||
|- | |||
| <center>'''1866'''</center> | |||
| Gregor Mendel ... | |||
|- | |- | ||
| Line 37: | Line 356: | ||
|- | |- | ||
| <center>'''~1894'''</center> | | <center>'''~1894'''</center> | ||
| | | J.B.S. states: ''"I suppose my scientific career began at the age of about two, when I used to play on the floor of his laboratory and watch him playing a complicated game called "experiments"-the rules I did not understand, but he clearly enjoyed it."'' <ref name=haldaneautobio>Haldane JBS. (1966) An autobiography in brief. ''Perspectives in Biology and Medicine'' Summer. (The editors noted: "Professor Haldane died December 1, 1964. This article is reprinted with the kind permission of the illustrated Weekly of India, Bombay.")</ref> | ||
|- | |- | ||
| <center>'''1896'''</center> | | <center>'''1896'''</center> | ||
| | | Birth of J.B.S.'s sister, Naomi; later becomes Lady Mitichison | ||
|- | |- | ||
| Line 48: | Line 367: | ||
|- | |- | ||
| | | <center>'''~1900-1906'''</center> | ||
| | | J.B.S. states: ''"At the age of eight or so I was allowed to take down numbers which I called out when reading the burette of a gas-analysis apparatus and later to calculate from these numbers the amounts of various gases in a sample. After this I was promoted to making up simple mixtures for his use and, still later, to cleaning apparatus."'' <ref name=haldaneautobio>Haldane JBS. (1966) An autobiography in brief. ''Perspectives in Biology and Medicine'' Summer. (The editors noted: "Professor Haldane died December 1, 1964. This article is reprinted with the kind permission of the illustrated Weekly of India, Bombay.")</ref> | ||
|- | |||
| <center>'''~1901'''</center> | |||
| At age 8 years, J.B.S. accompanies his father to attend a lecture by the British experimental geneticist, Arthur Dukinfield Darbishire (1879–1915), reportedly on Mendel’s laws of inheritance, but possibly also on an opposing view of heredity, given Darbishire’s years of work attempting to reconcile the two views, the biometric and Mendelian views. <ref>Ankeny RA (2004) [http://dx.doi.org/10.1023/A:1004750216919 Marvelling at the Marvel: The Supposed Conversion of A.D. Darbishire to Mendelism.] ''Journal of the History of Biology'' 33:315-347.</ref> | |||
|- | |- | ||
| | | <center>'''~1904+'''</center> | ||
| | | J.B.S. states: ''"After I was twelve, he [J.B.S.'s father] discussed with me all his research before publication, and sometimes tried out a lecture course on me before delivering it to students."'' <ref name=haldaneautobio>Haldane JBS. (1966) An autobiography in brief. ''Perspectives in Biology and Medicine'' Summer. (The editors noted: "Professor Haldane died December 1, 1964. This article is reprinted with the kind permission of the illustrated Weekly of India, Bombay.")</ref> | ||
|- | |- | ||
| | |align=center|'''1912''' | ||
| | |align=left|J.B.S. at age 19 or 20, publishes his first scientific paper, on human respiratory physiology, co-authored with his father J.S. Haldane and his father’s collaborator, C.G. Douglas. | ||
|- | |- | ||
| Line 321: | Line 644: | ||
|} | |} | ||
| | |||
|} | |||
==TIMETABLE OF EVENTS PERTINENT TO THE LIFE, WORK AND TIMES OF J. B. S. HALDANE (referred in this chronology as J.B.S.)== | ==TIMETABLE OF EVENTS PERTINENT TO THE LIFE, WORK AND TIMES OF J. B. S. HALDANE (referred in this chronology as J.B.S.)== | ||
| Line 350: | Line 674: | ||
|- | |- | ||
|align=center|'''~1901''' | |align=center|'''~1901''' | ||
|align=left|At age 8 years, J.B.S. accompanies his father to attend a lecture by the British experimental geneticist, Arthur Dukinfield Darbishire (1879–1915), reportedly on Mendel’s laws of inheritance, but possibly also on an opposing view of heredity, given Darbishire’s years of work attempting to reconcile the two views.<ref>Ankeny RA (2004) [http://dx.doi.org/10.1023/A:1004750216919 Marvelling at the Marvel: The Supposed Conversion of A.D. Darbishire to Mendelism.] ''Journal of the History of Biology'' 33:315-347.</ref> | |align=left|At age 8 years, J.B.S. accompanies his father to attend a lecture by the British experimental geneticist, Arthur Dukinfield Darbishire (1879–1915), reportedly on Mendel’s laws of inheritance, but possibly also on an opposing view of heredity, given Darbishire’s years of work attempting to reconcile the two views, the biometric and Mendelian views.<ref>Ankeny RA (2004) [http://dx.doi.org/10.1023/A:1004750216919 Marvelling at the Marvel: The Supposed Conversion of A.D. Darbishire to Mendelism.] ''Journal of the History of Biology'' 33:315-347.</ref> | ||
|- | |- | ||
|align=center|'''~1904+''' | |align=center|'''~1904+''' | ||
| Line 806: | Line 1,130: | ||
| | | | ||
|} | |} | ||
==Atomic orbital tbl== | |||
{|align="center"} | |||
| | |||
{| class="prettytable" | |||
| colspan="8" | <center>'''Table: Features of Atomic Structure in Relation to Orbitals '''</center> | |||
|- | |||
| <center>'''Shell #'''</center> | |||
<center>'''''n'''''</center> | |||
| <center>'''Subshell'''</center> | |||
<center>'''Number'''</center> | |||
<center>'''''l'''''</center> | |||
| <center>'''Number of'''</center> | |||
<center>'''Orbitals in'''</center> | |||
<center>'''Subshell'''</center> | |||
| <center>'''Orbital Type '''</center> | |||
<center>'''(Subshell Notation)'''</center> | |||
| <center>'''Number of Orbitals'''</center> | |||
<center>'''per Subshell'''</center> | |||
| <center>'''Orbital Label'''</center> | |||
| <center>'''Number of Electrons '''</center> | |||
<center>'''Needed to Fill Subshell'''</center> | |||
| <center>'''Total Number of '''</center> | |||
<center>'''Electrons in Subshell'''</center> | |||
|- | |||
| <center>1</center> | |||
| <center>0</center> | |||
| <center>1</center> | |||
| <center>1s</center> | |||
| <center>1</center> | |||
| <center>1s</center> | |||
| <center>2</center> | |||
| <center>2</center> | |||
|- | |||
| <center>2</center> | |||
| <center>0</center> | |||
<center>1</center> | |||
| <center>1</center> | |||
<center>3</center> | |||
| <center>2s</center> | |||
<center>2p</center> | |||
| <center>1</center> | |||
<center>3</center> | |||
| <center>2s</center> | |||
<center>2p<sub>x</sub> 2p<sub>y</sub> 2p<sub>z </sub></center> | |||
| <center>2</center> | |||
<center>6</center> | |||
| <center>8</center> | |||
|- | |||
| <center>3</center> | |||
| <center>0</center> | |||
<center>1</center> | |||
<center>2</center> | |||
| <center>1</center> | |||
<center>3</center> | |||
<center>5</center> | |||
| <center>3s</center> | |||
<center>3p</center> | |||
<center>3d</center> | |||
| <center>1</center> | |||
<center>3</center> | |||
<center>5</center> | |||
| <center>3s</center> | |||
<center>3p<sub>x</sub> 3p<sub>y</sub> 3p<sub>z </sub></center> | |||
<center>3d<sub>xy</sub> 3d<sub>xz</sub> 3d<sub>yz</sub> 3d<sub>x</sub><sup>2</sup><sub>y</sub><sup>2 </sup>3d<sub>x</sub><sup>2</sup></center> | |||
| <center>2</center> | |||
<center>6</center> | |||
<center>10</center> | |||
| <center>18</center> | |||
|- | |||
| <center>4</center> | |||
| <center>0</center> | |||
<center>1</center> | |||
<center>2</center> | |||
<center>3</center> | |||
| <center>1</center> | |||
<center>3</center> | |||
<center>5</center> | |||
<center>7</center> | |||
| <center>4s</center> | |||
<center>4p</center> | |||
<center>4d</center> | |||
<center>4f</center> | |||
| <center>1</center> | |||
<center>3</center> | |||
<center>5</center> | |||
<center>7</center> | |||
| <center>4s</center> | |||
<center>4p<sub>x</sub> 4p<sub>y</sub> 4p<sub>z </sub></center> | |||
<center>4d<sub>xy</sub> 4d<sub>xz</sub> 4d<sub>yz</sub> 4d<sub>x</sub><sup>2</sup><sub>-y</sub><sup>2</sup> 4d<sub>z</sub><sup>2</sup></center> | |||
<center>See f orbital labels here</center> | |||
| <center>2</center> | |||
<center>6</center> | |||
<center>10</center> | |||
<center>14</center> | |||
| <center>32</center> | |||
|- | |||
| colspan="8" |''n'' = the principal quantum number, designating shell #s of increasing energy levels as more energy must be absorbed to maintain electrons more distant from the positively charged nucleus; ''l'' = the angular momentum of the orbitals segregating them into subshells numbered as ''l'', which increases monotonically. | |||
|} | |||
| | |||
|} | |||
{|align="left"} | |||
| | |||
xxxxx | |||
| | |||
|} | |||
==References== | |||
====Citations and Notes==== | |||
<div class="references-small"> | |||
<references /> | |||
</div> | |||
Latest revision as of 01:52, 22 November 2023
The account of this former contributor was not re-activated after the server upgrade of March 2022.
article test
ABSTRACT
The potential link between dietary sodium chloride (NaCl) intake, hypertension and osteoporosis has been speculated upon for years. Increased NaCl intake is associated with increases in blood pressure in metabolic balance studies as well as in population studies.
Acute NaCl infusions are known to induce a hyperchloremic metabolic acidosis. Accumulating clinical and epidemiologic data suggest that chronic low-grade diet- and age-related metabolic acidosis increase bone resorption and loss of bone mass.
Acute NaCl loading inhibits endothelial nitric oxide synthase in a dose-dependent manner in cell systems and transfected cell lines. Asymmetric dimethylarginine (ADMA) also inhibits the conversion of L-arginine to nitric oxide. Nitric oxide (NO) is a direct vasodilator, and decreases in NO production are associated with higher blood pressures.
Subjects who are particularly sensitive to salt, defined as an increase in mean arterial pressure (MAP) of at least 5 mmHg after an increase in dietary salt intake from 30 to 250 mmol/day, have increased levels of ADMA, resulting in less nitric oxide production, leading to higher blood pressures. In addition, on high salt diets, salt sensitive subjects have increased urinary calcium excretion compared to salt resistant subjects.
Those considerations raise the possibility that salt sensitivity is the key to predicting who, on a high NaCl diet, would be particularly prone to developing not only high blood pressure, but increased bone breakdown which can predispose to osteoporosis.
NaCl, METABOLIC ACIDOSIS AND BONE
Metabolic acidosis in in vitro studies induces increased osteoclast activation and bone resorption, decreased osteoblast activation and bone mineralization and increased calcium loss from bone as the systemic pH decreases,.. Bushinsky et al. have elegantly demonstrated in mouse calvarie that urine calcium efflux from bone dose-dependently increases as the systemic pH and plasma bicarbonate concentration decrease, whether the bone cells are alive, dead or stimulated with PTH or vitamin D. This group has also recently shown that OGR-1 is the proton sensing receptor on the osteoblasts that induces activation of the osteoclasts in a high acid environment.
Cross-sectional analyses of human metabolic balance studies demonstrate that increased ingestion of dietary NaCl is independently associated with lower steady-state blood pH (increased acid levels) and lower steady-state plasma bicarbonate levels within the range considered to be normal, (viz. a low grade chronic metabolic acidosis) compared with ingestion of a lower dietary NaCl intake. This effect is independent of the diet net acid load, renal function and the partial pressure of carbon dioxide, the three other variables that have been shown to regulate systemic pH and bicarbonate.
The dose-dependent effects of NaCl on acid production and excretion are even more pronounced in salt-sensitive rats. Batlle et al. demonstrated in Dahl/Rapp salt sensitive and salt resistant rats not only that urine net acid excretion (NAE) increased as NaCl intake increased, but that the NAE increases in the salt sensitive rats was significantly greater than in the salt resistant rats at all levels of salt intake. In other words, the salt sensitive rats had more of a metabolic acidosis with any salt intake than the salt resistant rats.
More recently, a small prospective study in young healthy subjects has demonstrated that dietary NaCl increases this low grade chronic metabolic acidosis in a dose-dependent fashion and this is associated with significant dose dependent increases in urinary excretion of calcium and of bone resorption markers such as C-telopeptide. Sharma et al. has also shown that salt sensitive humans had significantly lower blood pH and plasma bicarbonate levels on high salt diets compared to salt resistant subjects. Whether salt sensitive subjects also have greater urinary calcium or bone breakdown marker concentrations would be predicted, but has not been demonstrated.
NaCl AND NITRIC OXIDE SYNTHESIS
Nitric oxide (NO) is generated from L-arginine by the enzyme nitric oxide synthase. In vascular endothelial cells, nitric oxide is a direct vasodilator, leading to decreased blood pressure. Recently, NaCl has also been shown to dose-dependently decrease endogenous nitric oxide synthase (eNOS) activity in both bovine aortic endothelial cells (BAEC) as well as transfected Chinese hamster ovarian cells (CHO-eNOS). This effect seems to be mediated by the sodium ion, as NaPO4 [comment: PO4 trivalent, so formula would read Na3PO4, unless H2PO4 intended, in which case NaH2PO4 would yield acidic medium, I think.] also dose-dependently decreased eNOS activity.
Asymmetric dimethylarginine (ADMA), which derives from the methylation of arginine residues in proteins, is a competitive inhibitor of eNOS, and increases in ADMA inhibit nitric oxide related vasodilation, leading to increased blood pressure. In 13 salt sensitive normotensive subjects, Fang el al. demonstrated significantly higher mean blood pressures and ADMA levels on a high salt diet, compared to a low salt diet and compared to 47 salt resistant subjects on either salt diet.
NITRIC OXIDE AND BONE
Interestingly, several recent clinical studies have suggested that giving nitrates [explain relation of nitrates and nitric oxide] will improve bone mineral density., A recent comparison study by Nabhan and Rabie demonstrated in 60 postmenopausal women with osteoporosis that 12 months treatment with isosorbide dinitrate 20 mg daily was as effective as alendronate 70 mg weekly in improving bone mineral density (BMD) and DEXA T-score (10.8% vs. 12.1% respectively; p<0.05 for each within group increase, p=0.7 for between group differences).
Nitric oxide synthases have been demonstrated in both osteoclasts and osteoblasts. Rats that are deficient for the eNOS gene have significant reduction in bone formation. Nitric oxide produced by bone cells may play an important role in mechanical-strain induced bone remodeling..
Nitric oxide may also be the mediator by which estrogen or androgen therapy improves BMD. Studies in castrated or oophorectomized rats given the NOS blocker L‑NAME demonstrated no loss of the usual sex-steroid-deficiency-induced BMD compared to the rats not given L-NAME. [do not follow this reasoning]
SALT SENSITIVITY AND BONE METABOLISM
From the previous paragraphs, dietary NaCl would be expected to affect bone metabolism in two ways; by inducing a low grade metabolic acidosis and by inhibiting nitric oxide production. The data also suggests that these effects will be seen especially in those subjects who are salt sensitive. Schmidlin et al. studied the effects of NaCl intake in 47 salt-sensitive (SS) and salt-resistant (SR) normotensive subjects on blood pressure, ADMA production and urine calcium excretion on both a low (30 mmol/day) salt and a high (250 mmol/day) diet in a 2 week crossover metabolic balance study. As expected, NaCl loading induced a significant increase in mean arterial pressure (MAP) in the SS but not in the SR subjects, associated in increases in ADMA only in the SS group, p=0.007. ADMA levels were significantly correlated with urine calcium excretion only in the salt sensitive group (R2=0.47, p=0.02), with no correlation in the SR group (R2=0.03, p=0.57). Urine pH?….
Studies suggest that subjects with risk factors for metabolic syndrome are also more likely to be salt sensitive. Chen et al. studied 1881 subjects in northern China and evaluated them for salt sensitivity as well as the presence of markers for the metabolic syndrome; dyslipidemia, abdominal obesity, hyperglycemia and elevated blood pressure. After adjustment for age, sex, education, physical activity, cigarette smoking, body mass index and 24-hour urinary sodium and potassium excretion, there was a progressive increase in the relative risk for salt sensitivity as the number of risk factors for metabolic syndrome increased (four or five factors; OR 3.54, CI 2.05-6.11). Metabolic syndrome has been associated with lower urine pH values and lower nitric oxide levels. [relevance to osteoporosis? No mention of bone.]
Conversely, subjects who are insensitive to salt, such as those with mutations leading to renal salt wasting, might be expected to have less salt-induced bone resorption. Cruz et al. has shown that subjects who are homozygous for the NCCT mutation (of the thiazide sensitive Na-Cl transporter in the distal tubule in the kidney) have significantly higher serum bicarbonate levels, lower urine calcium excretion associated with higher urine Na excretion, and higher BMDs than subjects who are heterozygous for the mutation, and both groups are higher than subjects who are homozygous for the wild-type alleles.
COMMON FINAL PATHWAY?
Is there a relationship between metabolic acidosis and nitric oxide synthesis? Studies by Mitch et al. over the last decade have demonstrated that in muscle cells metabolic acidosis inhibits the signaling pathway for insulin and IGF-1, leading to decreased intracellular phosphoinositol-3-kinase (PI3K) activity, which in turn leads to activation of nuclear factors, caspase-3 activity and increased protein degradation. In endothelial cells, IGF-1 is the receptor that activates PI3K leading to increased nitric oxide synthesis.
NaCl, then, might in fact have a “double whammy†effect on bone; 1) by inducing a metabolic acidosis and 2) by inhibiting NO production, the latter resulting perhaps separately from metabolic acidosis (inhibiting IGF-1 signalling) and from salt loading (enhancing ADMA levels). Those subjects who are particularly sensitive to the effects of NaCl would be those subjects most likely to demonstrate increased bone breakdown and decreased BMD. This hypothesis would help solidify the previously speculated upon but unproven relationship between hypertension and osteoporosis, and perhaps other metabolic disease, such as diabetes and metabolic syndrome, and osteoporosis.
CONCLUSIONS
To review the points that have been covered in this manuscript:
- NaCl intake dose-dependently induces increased degrees of metabolic acidosis and high blood pressure, independently of known acidosis-producing factors;
- NaCl stimulates ADMA, which reduces NO levels, and correlates with higher blood pressure in all subjects; and, in SS subjects increases urinary calcium excretion, the latter potentially due to increased net bone resorption.
- Thus, in SS subjects increased NaCl intake induces a metabolic acidosis and reduces NO synthesis, a “DOUBLE JEOPARDY†resulting in pressor and osteoporotic effects.
[summary should expand to cover all the main pathophysiological connections discussed in paper.]
[Very original and sophisticated synthesis – think NIH grant, NaCl reduction to eliminate two big killers of elderly, or KBC to counteract the effect of NaCl, as a natriuretic and chlouretic, and as an acid neutralizer.]
dalton image

Mole (Chemistry)
Chemists employ standard units of measurement to characterize samples of the substances they study. For example:
- they use the basic unit designated liter (abbr., L) to characterize the volume of the sample, viz., the amount of three-dimensional space the sample occupies. Under the same conditions, 1.45 L of water occupies the same volume as 1.45 L of ethanol (drinking alcohol).
- they use the basic unit designated kilogram (abbr., kg) to characterize the mass of the sample, viz., the quantity of matter in the sample as reflecting the force required to accelerate it (force equals mass times acceleration, F=ma). 1.52 kg of water contains the same mass of matter as 1.52 kg of ethanol.
Often chemists want to characterize a sample of a substance by a unit of measurement that represents the number of molecules the sample contains. Here we will discuss that unit in relation to pure substances, e.g., those that contain only one type of molecule, as in the case of samples of pure water, pure glucose, pure dioxygen, etc. — namely, chemical compounds.
For the purpose, chemists invented the basic unit designated mole. Just as equal liters of different chemical compounds occupy the same volume, and equal masses of different chemical compounds contain the same quantity of matter, equal moles of different chemical compounds contain the same number of molecules.
Without a deep understanding of the concept and application of the mole, one cannot exploit chemistry to develop understanding biology and medicine, or to produce industrial and technological advances.
In this article, we will describe how chemists define the unit, mole, in a way that allows it to reflect the number of molecules in a sample of a chemical compound; how they determine the number of moles in a sample; how they use the unit to characterize chemical reactions and for many other purposes; and how they extend use of the unit to samples of chemical elements and of other types of pure chemical substances besides compounds and elements
Creeping up on moles
What do we need to know to understand the concept of mole?
- the definition of mass
- the standard units of mass, including the units of mass of atoms
- the definitions of molecule and chemical compound
- the masses of the atoms of the elements
- what an isotope means
- the relative abundances of the various isotopes of an element
- how to calculate the number of molecules in a sample of a chemical compound
The mass of single atoms of the chemical elements
A molecule of a chemical compound consists of two or more different types of atoms (e.g., hydrogen and oxygen atoms when considering a water molecule) bound together in a fixed ratio per molecule (e.g., two hydrogen atoms to one oxygen atom per molecule of water). To understand how the unit of measurement, mole, gives a representation of the number of molecules in a sample of a chemical compound (e.g., 1.0 L of water; 1.0 kg of dioxygen gas), we first need to know the masses of the atoms that make up the sample.[1] Each of the 92 different types of atoms (making up the 92 naturally-occurring elements) has a different 'mass number', referred to as the atomic mass number. Moreover, the atoms of many elements exist as multiple 'isotopes' that have differing number of neutrons, hence in atomic mass number, accompanying their element-unique number of protons and electrons.
Using atomic mass numbers to calculate the number of molecules in samples of chemical compounds
If we knew the mass numbers of the different types of atoms in a chemical compound, [2] the relative abundance and mass numbers of the several isotopes of those element’s atoms, the ratio of the different types of atoms making up the molecules of the chemical compound, and the total mass of the sample of the chemical compound, we could, with simple algebra, calculate the number of molecules in the sample.
Consider 1.0 g (1/1000th of a kg) of water, each molecule of which consists of two hydrogen atoms and one oxygen atom. Almost all hydrogen atoms exist as the isotope that has one proton and one electron (no extra neutrons), each atom with a mass of 1.674 x 10-21 kg, or 1.674 x 10-24 g, where one g equals 1/1000th of a kg (=10-3 kg). Almost all oxygen atoms exist as the isotope that has eight protons, eight neutrons, and eight electrons, designated O-16, each atom with a mass of 2.655 x 10-23 g. Ignoring the minor isotopes, and considering that water consists of two hydrogen atoms and one oxygen atom per molecule, we calculate the mass of a molecule of water as 2 x 1.674 x 10-24 + 2.655 x 10-23, or 2.990 x 10-23 g/molecule. 1.0 g of water then must contain (1.0 g /2.990 x 10-23 g/molecule), or 3.34 x 1022 molecules.
Scaling up atomic mass numbers for convenience: the 'atomic mass unit'
From the previous section we can conclude that a fifth of a teaspoon of water (~1.0 g) contains about 300 billion times more molecules than the number of stars in our galaxy, a consequence of the minute masses of its atoms. In fact, for all elements, atomic mass numbers range from about 10<sup-24 to 10<sup-22 g, all very minute. For convenience, chemists minimize dealing with such small numbers by defining a unit that serves as a marker, or conversion factor, for the atomic mass numbers. They call it the “atomic mass unit” (abbr., amu), and define it as 1/12 of the mass of one atom of the most abundant isotope of carbon, carbon-12 (6 protons, 6 neutrons, six electrons), the latter equal to 1.9926 x 10-23 g, 1/12th of which equals 1.6605 x 10-24 g. Thus,
Using that formula as a conversion factor, one can compute how many atomic mass units (amu’s) for any atom, knowing the atom’s mass number. O-16, with a mass number as mentioned of 2.655 x 10-23 g, must have [(2.655 x 10-23 g/atom)/1.6605-24 g/amu)] amu, or 15.99 amu. Thus, an oxygen atom has a mass of 15.99, expressed as atomic mass units. Knowing the conversion formula, we can always get back to oxygen’s mass in grams.
Converting atomic mass numbers to atomic mass units still allows us to determine the number of molecules in a sample of a chemical compound. We use the same procedure as we employed using atomic mass numbers, except now we use the more convenient small numbers of atomic mass units.
The minor isotopes: a little more chemistry before we can grasp the mole
Ignoring the minor isotopes of the atoms in the molecule of a chemical substance, as we did in the earlier example of calculating the number of molecules in a sample of a chemical compund, will not allow us to accurately calculate the number of molecules in the sample. Without incorporating them, we will not know the average atomic mass of a given atom type that has isotopes with slightly differing atomic mass units. To incorporate all of an element’s isotopes in getting the element’s atoms’ average atomic mass we must know the atomic mass units of each isotope, as well as its relative abundance among all the isotopes of the element. With a little algebra, we can then calculate the average mass of the atoms of a given element, and express the results in atomic mass units, for convenience.
Logically we would call the result the atomic mass of the element’s atoms, averaged out for all of the element’s isotopes. However, by tradition chemists call the result the atomic weight (AW) of the element’s atoms, the number we find in the periodic table.
For a simple example of how to calculate the atomic weight of an element, consider the element, oxygen. Oxygen has three naturally occurring isotopes of its atoms: O-16, amu=15.99491463, abundance=99.757%; O-17, amu=16.9991312, abundance=0.038%; O-18, amu=17.9991603, abundance=0.205%. We can calculate how much each isotope contributes the mass of the element’s atoms by the product of its fractional abundance and its atomic mass expressed in atomic mass units. By adding together those products we then get atomic mass of the element’s atoms averaged among the several isotopes, as if all the atoms had the same atomic mass. For oxygen, the calculation can be written as:
We see that number as the atomic weight of oxygen in the periodic table.
Grasping the mole
We now have nearly all we need to grasp the concept of mole. We just need a formal definition of mole. In defining the mole, chemists have done something similar to defining atomic mass units: they devised a definition that allow expressing large numbers (e.g., 1020) of molecules in convenient small numbers.
Without background of history or rationale at this point, we give the formal definition of mole:
One mole (of any chemical compound, say) equals the number of atoms in exactly 12 g of the major isotope of carbon, carbon-12.
- That definition tells us immediately that one mole of every chemical compound has the same number of molecules as the number of atoms in one mole, or 12 g, of carbon-12.
Just how many atoms does one mole, or 12 g, of cabon-12 have? We showed in an earlier section how to calculate the number of molecules in a given sample of a chemical compound. We can use the same method for determining how many atoms in a given sample, 12 g, of carbon-12.
- First we obtain from an appropriate look-up table the mass (i.e., atomic mass number) of one atom of carbon-12. We obtain 1.9926 x 10-23 g/ carbon-12 atom.
- Our sample contains 12 g carbon-12 atoms.
- For 12 g carbon-12, and 1.9926*10<su>-23 g per carbon-12 atom, with grams cancelling out, we can write:
- 12 g carbon-12/1.9226*10-23 g/carbon-12 atom = 6.022*1023 carbon-12 atoms
Thus, 12 g carbon-12 contains 6.022*1023 atoms.
Since the number of atoms in 12 g carbon-12 by definition equals one mole of carbon-12, and one mole of any chemical compound has the same number of molecules as does one mole of carbon-12, one mole of any chemical compound contains 6.022*1023 molecules.
Although chemists define the mole in terms of carbon atoms, the mole unit (6.022*1023 carbon atoms) applies to any sample of a pure substance (chemical compounds, atoms, ion, electrons, quanta, etc.) — each of which contains 6.022*1023 of its constituents, just as one score means 20 of any item (see Gettysburg Address) and one dozen means 12 of any item. In the chemistry of pure substances one mole means 6.022*1023 of any constituent.
If we remember that we can interconvert atomic mass numbers, ranging from 10-22 to 10-24 g, to atomic mass units (amu’s), ranging more conveniently from ~1 to ~240 amu, we can also use amu’s to calculate the number of items in one mole.
- One amu = 1/12th of the atomic mass number of one carbon-12 atom, the latter equal to 1.9926*10-23, 1/12th of which equals 1.6605*10-24 g (viz., .9926*10-23 g/12).
- Since one amu is 1/12th the atomic mass number of one carbon-12 atom, that means one carbon-12 atom has a mass in amu’s 12 times that, or precisely 12 amu.
- The number of atoms in a sample of 12 g carbon-12 then computes as:
Again, then 12 g carbon-12, or one mole of carbon-12, has 6.022*1023 atoms.
Chemists call the number of constituent items in one mole of an element or chemical compound Avogadro’s number
To repeat, 1 mole of atoms of every element equals 6.022*1023 atoms, and one mole of a sample of any pure substance (molecules, ions, electrons, radicals, quanta, etc.) likewise contains 6.022*1023 of its constituent items.
Chemists refer the number 6.022*1023 as Avogadro’s Number (NA), after the pioneering physicist, Amedeo Avogadro (1776-1856), who first recognized the distinction between atoms and molecules. To get a sense of the size of Avogadro’s number, the Oxford chemist, Peter Atkins called attention to the visualization that with an Avogadro’s number, one mole, of soft-drink cans one could cover the surface of the earth with a pile 200 miles high.
Use this from SI Brochure
SI brochure, Section 2.1.1.6
Following the discovery of the fundamental laws of chemistry, units called, for example, "gram-atom" and "gram-molecule", were used to specify amounts of chemical elements or compounds. These units had a direct connection with "atomic weights" and "molecular weights", which are in fact relative masses. "Atomic weights" were originally referred to the atomic weight of oxygen, by general agreement taken as 16. But whereas physicists separated the isotopes in a mass spectrometer and attributed the value 16 to one of the isotopes of oxygen, chemists attributed the same value to the (slightly variable) mixture of isotopes 16, 17 and 18, which was for them the naturally occurring element oxygen. Finally an agreement between the International Union of Pure and Applied Physics (IUPAP) and the International Union of Pure and Applied Chemistry (IUPAC) brought this duality to an end in 1959/60. Physicists and chemists have ever since agreed to assign the value 12, exactly, to the so-called atomic weight of the isotope of carbon with mass number 12 (carbon 12, 12C), correctly called the relative atomic mass Ar(12C). The unified scale thus obtained gives the relative atomic and molecular masses, also known as the atomic and molecular weights, respectively.
The quantity used by chemists to specify the amount of chemical elements or compounds is now called "amount of substance". Amount of substance is defined to be proportional to the number of specified elementary entities in a sample, the proportionality constant being a universal constant which is the same for all samples. The unit of amount of substance is called the mole, symbol mol, and the mole is defined by specifying the mass of carbon 12 that constitutes one mole of carbon 12 atoms. By international agreement this was fixed at 0.012 kg, i.e. 12 g.
Following proposals by the IUPAP, the IUPAC, and the ISO, the CIPM gave a definition of the mole in 1967 and confirmed it in 1969. This was adopted by the 14th CGPM (1971, Resolution 3):
1. The mole is the amount of substance of a system which contains as many elementary entities as there are atoms in 0.012 kilogram of carbon 12; its symbol is "mol". 2. When the mole is used, the elementary entities must be specified and may be atoms, molecules, ions, electrons, other particles, or specified groups of such particles.
It follows that the molar mass of carbon 12 is exactly 12 grams per mole, M(12C) = 12 g/mol.
In 1980 the CIPM approved the report of the CCU (1980) which specified that
In this definition, it is understood that unbound atoms of carbon 12, at rest and in their ground state, are referred to.
The definition of the mole also determines the value of the universal constant that relates the number of entities to amount of substance for any sample. This constant is called the Avogadro constant, symbol NA or L. If N(X) denotes the number of entities X in a specified sample, and if n(X) denotes the amount of substance of entities X in the same sample, the relation is
n(X) = N(X)/NA.
Note that since N(X) is dimensionless, and n(X) has the SI unit mole, the Avogadro constant has the coherent SI unit reciprocal mole.
In the name "amount of substance", the words "of substance" could for simplicity be replaced by words to specify the substance concerned in any particular application, so that one may, for example, talk of "amount of hydrogen chloride, HCl", or "amount of benzene, C6H6". It is important to always give a precise specification of the entity involved (as emphasized in the second sentence of the definition of the mole); this should preferably be done by giving the empirical chemical formula of the material involved. Although the word "amount" has a more general dictionary definition, this abbreviation of the full name "amount of substance" may be used for brevity. This also applies to derived quantities such as "amount of substance concentration", which may simply be called "amount concentration". However, in the field of clinical chemistry the name "amount of substance concentration" is generally abbreviated to "substance concentration".
http://www.bipm.org/en/si/si_brochure/chapter2/2-1/mole.html
The 11th General Conference on Weights and Measures (1960) adopted the name Système International d'Unités (International System of Units, international abbreviation SI), for the recommended practical system of units of measurement.
The 11th CGPM laid down rules for the prefixes, the derived units, and other matters. The base units are a choice of seven well-defined units which by convention are regarded as dimensionally independent: the metre, the kilogram, the second, the ampere, the kelvin, the mole, and the candela. Derived units are those formed by combining base units according to the algebraic relations linking the corresponding quantities. The names and symbols of some of the units thus formed can be replaced by special names and symbols which can themselves be used to form expressions and symbols of other derived units.
The SI is not static but evolves to match the world's increasingly demanding requirements for measurement. The International System of Units (SI)
See also
- several sources, incl. hx
- Wichers 1962[3]
References [mole]
- ↑ Note: This discussion requires accepting the standard units of mass, including atomic mass, as established by international agreement.
- ↑ Note: Chemists have devised methods for determining the masses of atoms (e.g., mass spectroscopy) and have compiled lists of the mass numbers of the various isotopes of the naturally-occurring elements.
- ↑ Wichers E. (1962) New Scale of nuclidic masses and atomic weights. Nature 194:621-624.
test

xxx[1]
When someone writes history, we call that person a historian. When a historian of fervent curiosity bases the writing of history in particular on critical analysis of historical source material and provides a narrative synthesis that receives the approprobation of critical analysis, we may refer to the person more technically, and with more distinction, as a historiographer (etymologically a grapher of what one has learned through inquiry). We refer to the historiographer's writing of history as historiography — i.e., the historiographer's art or occupation. Thus, Herodotus, the Greek historian whose life nearly spanned the 5th century BCE, and whom the Roman scholar, Cicero (106-43 BCE), dubbed 'the father of history', occupied himself with the 'art' of historiography, writing of the wars of the Greeks and Persians — in the process setting a precedent for historiographers to come.
The term historioigraphy may apply, in another sense, to the study of historical writing, to the history of historical writing, and to the theoretical bases of historical writing, in contrast to the study of the history per se. The journal Histos ("The Electronic journal of ancient historiography at the university of Durham.") states that its ....focus will be more on the historical texts and media than on the historical problems for which those texts and media are sources, though the emphasis may naturally vary. For example, see the article by Clemence Schultze, entitled "Authority, originality and competence in the Roman Archaeology of Dionysius of Halicarnassus".[2]
Thus, a historiographer may write history or study how historiographers write history.
- ↑ Ilberg J. (1927) Sorani Gynaeciorum Libri N. De signis fracturarum. De fascUs. Vita Hippocratis secundum Soranum (CMG IV), Leipzig & Berlin.
- ↑ Schultze C. (2000) Authority, originality and competence in the Roman Archaeology of Dionysius of Halicarnassus. Histos Vol. 4, December
- Opening paragraph: Any attempt to understand an ancient historian’s programme, claim to authority, self-definition,[citation] originality and ideas about history and historiography must begin with analysis of his prefatory statements.[citation] Dionysius’ preface (whose literary and intellectual quality has generally been underestimated) reveals how his authority rests at once upon his predecessors and upon himself. At the very outset, in a single long and impressive sentence, he marks his knowledge of, and simultaneously his distance from, those predecessors; he expresses his attitude to his role and his materials; and he asserts the logismoi (‘reasonings’) and empeiria (‘knowledge’) which underpin his work: [Dionysius's sentence follows]
refs
Image test
Risks of Developing Osteoporosis in Women and Men
Fractures, a common consequence of osteoporosis, and often the first indication of the disease, rank as osteoporosis' most adverse consequence. It of causes severe pain and debilitation, especially in the elderly who fall and fracture their hip, and it can lead to death from complications during the planned recovery period. Some 20% of hip fracture patients die within a year (Leibson et al. 2002).
The 1.5 million osteoporotic fractures in the United States each year lead to more than half a million hospitalizations, over 800,000 emergency room encounters, more than 2,600,000 physician office visits, and the placement of nearly 180,000 individuals into nursing homes. Hip fractures are by far the most devastating type of fracture, accounting for about 300,000 hospitalizations each year (Surgeon General 2004).
The accompanying table from the Surgeon General's 2004 report (Surgeon General 2004) indicates that at age 50 years white women carry a lifetime risk of hip, spine or forearm fracture amounting to nearly 40%, and men about 13%.
The gender difference relates in part to the faster waning of sex steroid hormones in women as they age, menopause predating the more gradual andropause. Male and female sex hormones act on bone in a positive way, not surprisingly since successful reproduction depends in many ways on healthy bones in the parents.
References Cited
- Listed here in alphabetical order by last name of first author as cited with publication date in the text.
- Leibson CL, Tosteson AN, Gabriel SE, Ransom JE, Melton LJ. (2002) Mortality, disability, and nursing home use for persons with and without hip fracture: a population-based study. J Am Geriatr. Soc. 50(10):1644-50. PMID 12366617.
- Abstract: OBJECTIVES: To compare persons with and without hip fracture for subsequent mortality and change in disability and nursing home (NH) use. DESIGN: Population-based historical cohort study. SETTING: Olmsted County, Minnesota. PARTICIPANTS: All residents who experienced a first hip fracture between January 1, 1989, and December 31, 1993, and, for each case, a resident of the same sex and similar age who had not experienced a hip fracture and was seen by a local care provider. MEASUREMENTS: Data on disability (Rankin score), comorbidity (Charlson Index), and NH residency before baseline (fracture date for cases and registration date for controls) were obtained by review of complete community-based medical records. The records were then reviewed from baseline through December 31, 1994, for Rankin disability at 1 month and 1 year, all NH admissions and discharges, and date of death for those who died. RESULTS: There were 312 cases and 312 controls (81% female, mean age +/- standard deviation = 81 +/- 12 years). Before baseline, cases had higher comorbidity (45% vs 30% had Charlson Index >/= 1, P <.001) and disability (mean Rankin score = 2.5 +/- 1.1 vs 2.2 +/- 1.1, P <.001) and were more likely to be in a NH (28% vs 18%, P <.001) than controls. One year after baseline, estimated mortality was 20% (95% confidence interval (CI) = 16-24) for cases vs 11% (95% CI = 8-15) for controls, 51% of cases versus 16% of controls had a level of disability one or more units worse than before baseline (P <.001), and the cumulative incidence of first NH admission was 64% (95% CI = 58-71) for cases versus 7% (95% CI = 4-11) for controls. The risk of NH admission for cases relative to controls diminished over time, but remained elevated 5 years after the event (risk ratio = 20.0 at 3 months and 2.1 at 5 years), but, in persons admitted to a nursing home, cases were two times more likely than controls to be discharged alive within a year (P <.001). CONCLUSIONS: Hip fracture is an important contributor to disability and NH use, but the potential savings from hip fracture prophylaxis may be overestimated by studies that fail to consider differential risk, mortality, and long-term follow-up.
- Cummings SR, Melton LJ. (2002) Epidemiology and outcomes of osteoporotic fractures. Lancet 359(9319):1761-7 PMID 12049882.
- Abstract: Bone mass declines and the risk of fractures increases as people age, especially as women pass through the menopause. Hip fractures, the most serious outcome of osteoporosis, are becoming more frequent than before because the world's population is ageing and because the frequency of hip fractures is increasing by 1-3% per year in most areas of the world. Rates of hip fracture vary more widely from region to region than does the prevalence of vertebral fractures. Low bone density and previous fractures are risk factors for almost all types of fracture, but each type of fracture also has its own unique risk factors. Prevention of fractures with drugs could potentially be as expensive as medical treatment of fractures. Therefore, epidemiological research should be done and used to identify individuals at high-risk of disabling fractures, thereby allowing careful allocation of expensive treatments to individuals most in need.
- Surgeon General Report. (2004) Bone Health and Osteoporosis
Notes (numbered as footnotes in text)
Scientists
For biographies of scientists.
Table from OO
|
TIMETABLE OF EVENTS PERTINENT TO THE LIFE, WORK AND TIMES OF J. B. S. HALDANE (referred in this chronology as J.B.S.)
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||