imported>Paul Wormer |
imported>Paul Wormer |
| Line 1: |
Line 1: |
| {{subpages}} | | {{subpages}} |
| In [[analytic geometry]], a '''reflection''' is a linear operation σ on <font style="vertical-align: top"><math>\mathbb{R}^3</math></font> with σ<sup>2</sup> = E, the identity map. This property of σ is called ''involution''. An involutory operator is non-singular and σ<sup>−1</sup> = σ. Reflecting twice an arbitrary vector brings back the original vector : | | In [[Euclidean geometry]], a '''reflection''' is a linear operation σ on <font style="vertical-align: top"><math>\mathbb{R}^3</math></font> with σ<sup>2</sup> = E, the identity map. This property of σ is called ''involution''. An involutory operator is non-singular and σ<sup>−1</sup> = σ. Reflecting twice an arbitrary vector brings back the original vector : |
| :<math> | | :<math> |
| \sigma( \vec{\mathbf{r}}\,) = \vec{\mathbf{r}}\,' \quad\hbox{and}\quad \sigma( \vec{\mathbf{r}}\,'\,) = \vec{\mathbf{r}}. | | \sigma( \vec{\mathbf{r}}\,) = \vec{\mathbf{r}}\,' \quad\hbox{and}\quad \sigma( \vec{\mathbf{r}}\,'\,) = \vec{\mathbf{r}}. |
In Euclidean geometry, a reflection is a linear operation σ on  with σ2 = E, the identity map. This property of σ is called involution. An involutory operator is non-singular and σ−1 = σ. Reflecting twice an arbitrary vector brings back the original vector :
with σ2 = E, the identity map. This property of σ is called involution. An involutory operator is non-singular and σ−1 = σ. Reflecting twice an arbitrary vector brings back the original vector :

The operation σ is an isometry of  onto itself, which means that it preserves inner products and that its inverse is equal to its adjoint,
onto itself, which means that it preserves inner products and that its inverse is equal to its adjoint,

Hence reflection is also symmetric: σT = σ. From (det(σ))2 = det(E) = 1 follows that isometries have determinant ±1. Those with positive determinant are rotations, while reflections have determinant −1. Because σ is symmetric it has real eigenvalues; since the extension of an isometry to a complex space is unitary, its (complex) eigenvalues have modulus 1. It follows that the eigenvalues of σ are ±1. The product of the eigenvalues being its determinant, −1, the sets of eigenvalues of σ are either {1, 1, −1}, or {−1, −1, −1}. An operator with the latter set of eigenvalues is equal to −E, minus the identity operator. This operator is known alternatively as inversion, reflection in a point, or parity operator. An operator with the former set of eigenvalues is reflection in a plane. Reflections in a plane are the subject of this article.
Sometimes one finds the concept of "reflections in a line", these are rotations over 180°, see rotation matrix.
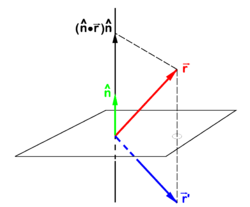
PD Image Fig. 1. The vector

goes to

under reflection in a plane. The unit vector

is normal to mirror plane.
Reflection in a plane
If  is a unit vector normal (perpendicular) to a plane—the mirror plane—then
is a unit vector normal (perpendicular) to a plane—the mirror plane—then  is the projection of
is the projection of  on this unit vector. From the figure it is evident that
on this unit vector. From the figure it is evident that

If a non-unit normal  is used then substitution of
is used then substitution of

gives the mirror image,

Sometimes it is convenient to write this as a matrix equation. Introducing the dyadic product, we obtain
![{\displaystyle {\vec {\mathbf {r} }}\,'=\left[\mathbf {E} -{\frac {2}{n^{2}}}{\vec {\mathbf {n} }}\otimes {\vec {\mathbf {n} }}\right]\;{\vec {\mathbf {r} }},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb112d732fbaf7c81a05f819922f6b4d713dc646)
where E is the 3×3 identity matrix.
Dyadic products satisfy the matrix multiplication rule
![{\displaystyle [{\vec {\mathbf {a} }}\otimes {\vec {\mathbf {b} }}]\,[{\vec {\mathbf {c} }}\otimes {\vec {\mathbf {d} }}]=({\vec {\mathbf {b} }}\cdot {\vec {\mathbf {c} }}){\big (}{\vec {\mathbf {a} }}\otimes {\vec {\mathbf {d} }}{\big )}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/037a6b38897a0d8a8d7787a0ea60a4e18d091281)
By the use of this rule it is easily shown that
![{\displaystyle \left[\mathbf {E} -{\frac {2}{n^{2}}}{\vec {\mathbf {n} }}\otimes {\vec {\mathbf {n} }}\right]^{2}=\mathbf {E} ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd65ff7a8f5970ebba0e77e1a5680c6192a28266)
which confirms that reflection is involutory.
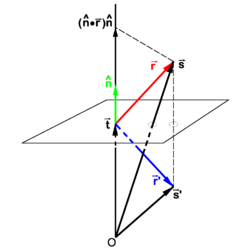
PD Image Fig. 2. The vector

goes to

under reflection
Reflection in a plane not through the origin
In Figure 2 a plane, not containing the origin O, is considered that is orthogonal to the vector  . The length of this vector is the distance from O to the plane.
From Figure 2, we find
. The length of this vector is the distance from O to the plane.
From Figure 2, we find

Use of the equation derived earlier gives

And hence the equation for the reflected pair of vectors is,

where  is a unit vector normal to the plane. Obviously
is a unit vector normal to the plane. Obviously  and
and  are proportional, they differ only by scaling. Therefore, the equation can be written solely in terms of
are proportional, they differ only by scaling. Therefore, the equation can be written solely in terms of  ,
,

Two consecutive reflections
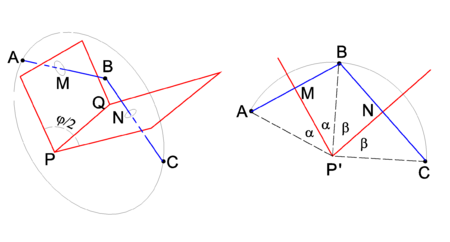
PD Image Fig. 3. Two reflections. Left drawing: 3-dimensional drawing. Right drawing: view along the PQ axis, drawing projected on the plane through ABC. This plane intersect the line PQ in the point P′
Two consecutive reflections in two intersecting planes give a rotation around the line of intersection. This is shown in Figure 3, where PQ is the line of intersection.
The drawing on the left shows that reflection of point A in the plane through PMQ brings the point A to B. A consecutive reflection in the plane through PNQ brings B to the final position C. In the right-hand drawing it is shown that the rotation angle φ is equal to twice the angle between the mirror planes. Indeed, the angle ∠ AP'M = ∠ MP'B = α and ∠ BP'N = ∠ NP'C = β. The rotation angle ∠ AP'C ≡ φ = 2α + 2β and the angle between the planes is α+β = φ/2.
It is obvious that the product of two reflections is a rotation. Indeed, a reflection is an isometry and has determinant −1. The product of two isometric operators is again an isometry and the rule for determinants is det(AB) = det(A)det(B), so that the product of two reflections is an isometry with unit determinant, i.e., a rotation.
Let the normal of the first plane be  and of the second
and of the second  , then the rotation is represented by the matrix
, then the rotation is represented by the matrix
![{\displaystyle \left[\mathbf {E} -{\frac {2}{t^{2}}}{\vec {\mathbf {t} }}\otimes {\vec {\mathbf {t} }}\right]\,\left[\mathbf {E} -{\frac {2}{s^{2}}}{\vec {\mathbf {s} }}\otimes {\vec {\mathbf {s} }}\right]=\mathbf {E} -{\frac {2}{t^{2}}}{\vec {\mathbf {t} }}\otimes {\vec {\mathbf {t} }}-{\frac {2}{s^{2}}}{\vec {\mathbf {s} }}\otimes {\vec {\mathbf {s} }}+{\frac {4}{t^{2}s^{2}}}({\vec {\mathbf {t} }}\cdot {\vec {\mathbf {s} }})\;{\big (}{\vec {\mathbf {t} }}\otimes {\vec {\mathbf {s} }}{\big )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/454d07547f582382357684b9dc6463f3ff0ecbbc)
The (i,j) element if this matrix is equal to

This formula is used in vector rotation.














![{\displaystyle {\vec {\mathbf {r} }}\,'=\left[\mathbf {E} -{\frac {2}{n^{2}}}{\vec {\mathbf {n} }}\otimes {\vec {\mathbf {n} }}\right]\;{\vec {\mathbf {r} }},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb112d732fbaf7c81a05f819922f6b4d713dc646)
![{\displaystyle [{\vec {\mathbf {a} }}\otimes {\vec {\mathbf {b} }}]\,[{\vec {\mathbf {c} }}\otimes {\vec {\mathbf {d} }}]=({\vec {\mathbf {b} }}\cdot {\vec {\mathbf {c} }}){\big (}{\vec {\mathbf {a} }}\otimes {\vec {\mathbf {d} }}{\big )}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/037a6b38897a0d8a8d7787a0ea60a4e18d091281)
![{\displaystyle \left[\mathbf {E} -{\frac {2}{n^{2}}}{\vec {\mathbf {n} }}\otimes {\vec {\mathbf {n} }}\right]^{2}=\mathbf {E} ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cd65ff7a8f5970ebba0e77e1a5680c6192a28266)









![{\displaystyle \left[\mathbf {E} -{\frac {2}{t^{2}}}{\vec {\mathbf {t} }}\otimes {\vec {\mathbf {t} }}\right]\,\left[\mathbf {E} -{\frac {2}{s^{2}}}{\vec {\mathbf {s} }}\otimes {\vec {\mathbf {s} }}\right]=\mathbf {E} -{\frac {2}{t^{2}}}{\vec {\mathbf {t} }}\otimes {\vec {\mathbf {t} }}-{\frac {2}{s^{2}}}{\vec {\mathbf {s} }}\otimes {\vec {\mathbf {s} }}+{\frac {4}{t^{2}s^{2}}}({\vec {\mathbf {t} }}\cdot {\vec {\mathbf {s} }})\;{\big (}{\vec {\mathbf {t} }}\otimes {\vec {\mathbf {s} }}{\big )}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/454d07547f582382357684b9dc6463f3ff0ecbbc)
