imported>Paul Wormer |
imported>Paul Wormer |
| (14 intermediate revisions by the same user not shown) |
| Line 1: |
Line 1: |
| '''Charles Marie de La Condamine''' (Paris, January 27, 1701 – Paris, February 4, 1774)
| | ==Parabolic mirror== |
| was a French geodesist, astronomer, and mathematician with strong interests in ethnography and botany. He spent ten years in present-day [[Ecuador]] measuring the length of the [[equator]] and preparing the first map of the [[Amazon]] region based on astronomical observations.
| | {{Image|Refl parab.png|right|350px|Fig. 2. Reflection in a parabolic mirror}} |
| ==Biography== | | Parabolic mirrors concentrate incoming vertical light beams in their focus. We show this. |
| Charles Marie de La Condamine was a son of well-to-do parents, Charles de La Condamine and Louise Marguerite Chourses. He studied at the [[Collège Louis-le-Grand]] where he was trained in humanities as well as in mathematics. After finishing his studies, he enlisted in the army and fought in the war against Spain (1719). After returning from the war, he became acquainted with scientific circles in Paris. On December 12, 1730 he became a member of the [[Académie des Sciences]] and was appointed Assistant Chemist at the Academy.
| |
|
| |
|
| The next year (May 1731) he sailed with the [[Levant Company]] to [[Constantinople]] (now [[Istanbul]]) where he stayed five months. After returning to Paris, La Condamine submitted in November 1732 a paper to the Academy entitled ''Mathematical and Physical Observations made during a Visit of the Levant in 1731 and 1732''.
| | Consider in figure 2 the arbitrary vertical light beam (blue, parallel to the ''y''-axis) that enters the parabola and hits it at point ''P'' = (''x''<sub>1</sub>, ''y''<sub>1</sub>). The parabola (red) has focus in point ''F''. The incoming beam is reflected at ''P'' obeying the well-known law: incidence angle is angle of reflection. The angles involved are with the line ''APT'' which is tangent to the parabola at point ''P''. It will be shown that the reflected beam passes through ''F''. |
|
| |
|
| Three years later he joined an expedition to present-day Ecuador that had the aim to test a hypothesis of [[Isaac Newton]]. Newton had posited that the Earth is not a perfect sphere, but bulges around the equator and is flattened at the poles. Newton's opinion had raised a huge controversy among French scientists. [[Maupertuis]], [[Clairaut]], and [[Le Monnier]] traveled to Lapland, where they were to measure the length of several degrees of longitude along the arctic circle, while [[Godin]], [[Bouguer]], and La Condamine were sent to South America to perform similar measurements along the [[equator]].
| | Clearly ∠''BPT'' = ∠''QPA'' (they are vertically opposite angles). Further ∠''APQ'' = ∠''FPA'' because the triangles ''FPA'' and ''QPA'' are congruent and hence ∠''FPA'' = ∠''BPT''. |
|
| |
|
| On May 16, 1735, La Condamine sailed from La Rochelle accompanied by Godin, Bougier, and a botanist [[Joseph de Jussieu]]. After stopovers in [[Martinique]], [[Santo Domingo]], [[Cartagena (Columbia)]], they came to Panama where they crossed the continent. Finally (March 10, 1736) the expedition arrived at the Pacific Port of [[Manta]] in the province of [[Quito]]. From Manta, Condamine took a route separate from Godin and Bouguer and joined them again on June 4, 1736 in the capital of the province, the city of Quito.
| | We prove the congruence of the triangles: By the definition of the parabola the line segments ''FP'' and ''QP'' are of equal length, because the length of the latter segment is the distance of ''P'' to the directrix and the length of ''FP'' is the distance of ''P'' to the focus. The point ''F'' has the coordinates (0,''f'') and the point ''Q'' has the coordinates (''x''<sub>1</sub>, −''f''). The line segment ''FQ'' has the equation |
| | | :<math> |
| The longitudinal arc that was chosen passed through a high valley perpendicular to the equator, stretching from Quito in the north to [[Cuenca]] in the south. The scientists spent a month performing triangulation measurements in the Yaruqui plains—from October 3 to November 3, 1736—and then returned to Quito. After they had come back in Quito, they found that subsidies expected from Paris had not come in. La Condamine, who had taken precautions and had made a deposit on a bank in [[Lima]], traveled early 1737 to Lima to collect money. He prolonged this journey somewhat to study the [[Cinchona tree]] with its medicinally active bark that was hardly known in Europe.
| | \lambda\begin{pmatrix}0\\ f\end{pmatrix} + (1-\lambda)\begin{pmatrix}x_1\\ -f\end{pmatrix}, \quad 0\le\lambda\le 1. |
| | | </math> |
| After returning to Quito on June 20, 1737, he found that Godin refused to disclose his results, whereupon La Condamine joined forces with Bouguer. The two men continued with their length measurements in the mountainous and inaccessible region close to Quito. When in December 1741 Bouguer, detected an error in a calculation of La Condamine, these two explorers got into a quarrel as well and stopped speaking to each other. However, working separately, the two completed their project in May 1743.
| | The midpoint ''A'' of ''FQ'' has coordinates (λ = ½): |
| | | :<math> |
| La Condamine chose to return by way of the Amazon River, a route which is longer and more dangerous. He reached the Atlantic Ocean at [[Para]] on September 19, 1743, having made on the way observations of astronomic and topographic interest. He also made some botanical studies, notably of Cinchona and Rubber trees. In February 1774 he arrived in [[Cayenne]], the capital of [[French Guiana]]. Finding no passage to France, he had to wait there for five months, but made good use of this time by observing and recording physical, biological, and ethnological phenomena. Leaving finally Cayenne in August 1744 he arrived in [[Amsterdam]] on November 30, 1744 from where it took him another two months to travel to Paris, arriving in February 1745. He brought with him many notes, natural history specimens, and art objects that he donated to the naturalist [[Georges-Louis Leclerc, Comte de Buffon|Buffon]] (1707–1788).
| | \frac{1}{2}\begin{pmatrix}0\\ f\end{pmatrix} + \frac{1}{2}\begin{pmatrix}x_1\\ -f\end{pmatrix} = |
| | | \begin{pmatrix}\frac{1}{2} x_1\\ 0\end{pmatrix}. |
| The scientific results of the expedition were unambiguous: the Earth is indeed a spheroid flattened at the poles as was believed by Newton. Not surprisingly, La Condamine and Bouguer failed to write a joint publication, it is Bouguer's death in 1758 that put an end to their quarrel. The other expedition member, Godin, died in 1760. The only surviving member, La Condamine, obtained most of the credits for the expedition that drew lots of attention in France. Although less talented in astronomy than Godin and a lesser mathematician than Bouguer, La Condamine was a gifted writer and popularizer. | | </math> |
| | | Hence ''A'' lies on the ''x''-axis. |
| La Condamine had contracted smallpox in his youth. This led him to take part in the debate on vaccination against the disease and to propagate vaccination. Assisted by the clarity and elegance of his writing, he presented several papers at the Academy of Sciences in which he defended his ideas with passion. He became a corresponding member of the academies of [[London]], [[Berlin]], [[Saint Petersburg]] and [[Bologna]] and was elected to the l'[[Académie française]] on November 29, 1760. In August 1756, he married, with papal dispensation, his young niece Charlotte Bouzia of Estouilly. La Condamine had many friends, the closest one being Maupertuis whom he bequeathed his papers. Condamine died in Paris February 4, 1774, following a hernia operation.
| | The parabola has equation, |
| | | :<math> |
| ==External link== | | y = \frac{1}{4f} x^2. |
| [http://www.academie-sciences.fr/archives/fonds_archives/Condamine/archives_Condamine_oeuvre.htm Biography of the Académie des Sciences]
| | </math> |
| | | The equation of the tangent at ''P'' is |
| ==Selected Works==
| | :<math> |
| *Observations mathématiques et physiques faites dans un voyage du Levant en 1731 et 1732.
| | y = y_1 + \frac{x_1}{2f} (x-x_1)\quad \hbox{with}\quad y_1 = \frac{x_1^2}{4f}. |
| *Relation abrégée d'un voyage, fait dans l'intérieur de l'Amérique méridional (1745)
| | </math> |
| *La figure de la terre déterminée (1749)
| | This line intersects the ''x''-axis at ''y'' = 0, |
| *Mesure des trois premiers degrés du méridien dans l'hémisphère australe (1751)
| | :<math> |
| *Journal du voyage, fait par ordre du roi, à l'équateur (1751)
| | 0 = \frac{x_1^2}{4f} - \frac{x_1^2}{2f} + \frac{x_1}{2f} x |
| | \Longrightarrow \frac{x_1}{2f} x = \frac{x_1^2}{4f} \longrightarrow x = \tfrac{1}{2}x_1. |
| | </math> |
| | The intersection of the tangent with the ''x''-axis is the point ''A'' = (½''x''<sub>1</sub>, 0) that lies on the midpoint of ''FQ''. The corresponding sides of the triangles ''FPA'' and ''QPA'' are of equal length and hence the triangles are congruent. |
Parabolic mirror
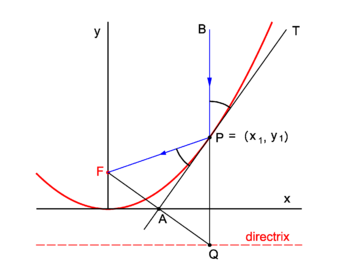
PD Image Fig. 2. Reflection in a parabolic mirror
Parabolic mirrors concentrate incoming vertical light beams in their focus. We show this.
Consider in figure 2 the arbitrary vertical light beam (blue, parallel to the y-axis) that enters the parabola and hits it at point P = (x1, y1). The parabola (red) has focus in point F. The incoming beam is reflected at P obeying the well-known law: incidence angle is angle of reflection. The angles involved are with the line APT which is tangent to the parabola at point P. It will be shown that the reflected beam passes through F.
Clearly ∠BPT = ∠QPA (they are vertically opposite angles). Further ∠APQ = ∠FPA because the triangles FPA and QPA are congruent and hence ∠FPA = ∠BPT.
We prove the congruence of the triangles: By the definition of the parabola the line segments FP and QP are of equal length, because the length of the latter segment is the distance of P to the directrix and the length of FP is the distance of P to the focus. The point F has the coordinates (0,f) and the point Q has the coordinates (x1, −f). The line segment FQ has the equation

The midpoint A of FQ has coordinates (λ = ½):

Hence A lies on the x-axis.
The parabola has equation,

The equation of the tangent at P is

This line intersects the x-axis at y = 0,

The intersection of the tangent with the x-axis is the point A = (½x1, 0) that lies on the midpoint of FQ. The corresponding sides of the triangles FPA and QPA are of equal length and hence the triangles are congruent.





