Acceleration due to gravity

Considering a body with the mass M as a source of a gravitational field, the strength of that field, or the gravitational acceleration, is given by ${\vec {g}}=-G{\frac {M}{r^{2}}}{\frac {\vec {r}}{r}}$. The modulus of g is $g=G{\frac {M}{r^{2}}}$.

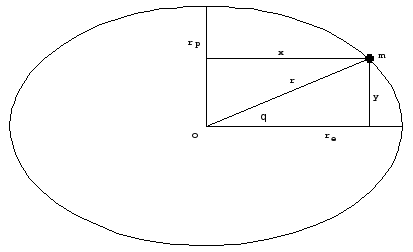
Here G is the gravitational constant, G = 6.67428×10^-11 Nm²/kg², r is the distance between a body of mass m and the center of the gravitational field, ${\vec {r}}$ is the vector radius of that body having the mass m. If the source of the gravitational field has a spherical shape, then r is the sphere’s radius. Taking into account that the Earth is an oblate spheroid, the distance r is not that of a sphere and varies from the equator to the poles.

A normal section (on the equatorial plane) is almost an ellipse, so, r can be done by:

$r={\sqrt {{r_{e}}^{2}cos^{2}\theta +{r_{p}}^{2}sin^{2}\theta }}$

where r_e and r_p are the equatorial radius and polar radius, respectively and θ is the latitude, or the angle made by r with the equatorial plane.

References

1. V.Dorobantu and Simona Pretorian, Physics between fear and respect, Vol. 3, Edited by Politehnica

                                         Timisoara, 2007, ISBN 978-973-625-493-2