Acceleration due to gravity: Difference between revisions
imported>'Dragon' Dave McKee No edit summary |
imported>'Dragon' Dave McKee mNo edit summary |
||
| Line 7: | Line 7: | ||
account that the Earth is an oblate spheroid, the distance ''r'' is not that of a sphere and varies from the | account that the Earth is an oblate spheroid, the distance ''r'' is not that of a sphere and varies from the | ||
equator to the poles. | equator to the poles. | ||
[[Image:OblateSpheroidAngles.png]] | |||
A normal section (on the equatorial plane) is almost an ellipse, so, ''r'' can be done by: | A normal section (on the equatorial plane) is almost an ellipse, so, ''r'' can be done by: | ||
Revision as of 20:15, 23 February 2008
Considering a body with the mass M as a source of a gravitational field, the strength of that field, or the gravitational acceleration, is given by . The modulus of g is .
Here G is the gravitational constant, G = 6.67428×10-11 Nm2/kg2, r is the distance between a body of mass m and the center of the gravitational field, is the vector radius of that body having the mass m. If the source of the gravitational field has a spherical shape, then r is the sphere’s radius. Taking into account that the Earth is an oblate spheroid, the distance r is not that of a sphere and varies from the equator to the poles.
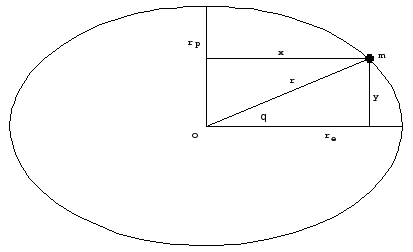 A normal section (on the equatorial plane) is almost an ellipse, so, r can be done by:
A normal section (on the equatorial plane) is almost an ellipse, so, r can be done by:
where re and rp are the equatorial radius and polar radius, respectively and θ is the latitude, or
the angle made by r with the equatorial plane.
References
1. V.Dorobantu and Simona Pretorian, Physics between fear and respect, Vol. 3, Edited by Politehnica
Timisoara, 2007, ISBN 978-973-625-493-2



