Work (physics)
In physics, work is the energy that is transferred to a body when it is moved along a path by a force. When the force is conservative (non-dissipative) the work is independent of the path. Work done on a body is accomplished not only by a displacement of the body as a whole from one place to another but also, for example, by compressing a gas, by rotating a shaft, and even by directing small magnetic particles within a body along an external magnetic field.
When Newton founded classical mechanics in his 1687 magnum opus Principia, he defined, of course, implicitly energy and work. However, it took more than a century before these concepts were recognized amidst the classical mechanics equations and seen as useful and worthy of independent consideration. A quantity close to kinetic energy was noticed quite early; Leibniz coined the name vis viva (live force) in 1695 for the quantity mv2 that—except for the factor ½— is what we now call kinetic energy. The fact that Leibniz used the name "vis", which usually was restricted to mean "force", shows that neither work (a form of energy, a scalar) nor force (a vector) were fully grasped concepts at that time.
The modern statement: "work is force times path" is due to French physicist Gustave-Gaspard Coriolis,[1] who gave the correct formula for change in kinetic energy associated with work, although he spoke of force vive (including the modern factor ½), instead of kinetic energy (the latter term was coined by William Thomson and Peter Guthrie Tait in their 1867 book Treatise on Natural Philosophy). Coriolis' terminology was taken over by Jean-Victor Poncelet who did much to propagate the terms "work" and "path", especially among engineers.[2]
Hence, since the early 19th century, the terms "work" and "energy" have well-defined, quantitative, meanings in physics, and both can be measured with a real number as outcome. The physics definitions are inspired by, but differ somewhat from, their more qualitative meanings in daily life. For instance, in physics work can be negative.
As stated, work is a form of energy and consequently it has the same dimension as energy [force times length, or mass times (length/time)2]. In SI units the unit is joule; in cgs units it is erg; in US units it is foot-pound.
Definition of mechanical work
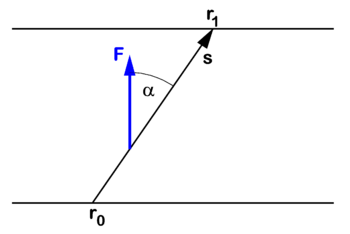
The mechanical work W is defined as force times path length: When a constant force F acts on a body along a straight path and the body is moved over a length |s| along this path, then
Here s is vector of magnitude |s| along the path. The dot product between the two vectors F and s is the product of their magnitudes |F| and |s| times the cosine of the angle (α) between them.
When the force is directed along the path (F and s parallel), α = 0, cosα = 1, and we have simply W = |F| |s|. The positive work W is converted into an increase of kinetic energy T,
- W = ΔT ≡ T1 − T0 > 0.
In the next section this relation will be proven and shown to be a consequence of Newton's second law: F = m a.
When a force is perpendicular to the path, α = 90°, cosα = 0, the force performs no work. Examples of such a situation are the centrifugal force on a mass in uniform circular motion and the gravitational force acting on a satellite in a circular orbit. If a body is in uniform (i.e., has constant speed) straight motion and the only force acting on it is perpendicular to its path, then the body will persist in its uniform straight motion (Newton's first law).
When a force F is anti-parallel to the path (α = 180°), it performs negative work W < 0, since cosα = −1, and |F| and |s| are both greater than zero. The negative work done by the force is converted into a decrease of the kinetic energy T,
- W = ΔT < 0
(ΔT < 0 because T decreases, i.e., T1 < T0).
For example, think of an old-fashioned type of cannon that shoots a cannon ball of mass m straight up. The gun powder explosion gives the ball initial kinetic energy T0 = ½ m v02. The gravitational attraction of the earth performs negative work (force downward, motion of the cannon ball upward), until at the highest point the speed v1 and the kinetic energy T1 = ½ m v12 of the ball are zero. The amount of work performed is W = ΔT = 0−T0 = −T0. At the highest point the motion of the cannon ball reverts direction, it starts falling to earth, and from there on the gravitational attraction performs positive work (direction of motion and force are parallel). The kinetic energy increases again until it achieves its original value T0 = ½ m v02 at the point where the cannon ball arrives again at the cannon. The total work done by the gravitation is zero, the work done on the cannon ball going up cancels the work done on the ball going down. (In this example we ignore friction by the air).
When the the force is conservative (non-dissipative), the work is independent of path, and when furthermore the path is a closed curve, the total work is zero (one way the work is positive and the other way the work is equally large in absolute value, but negative).
As the gravitational field is conservative, we just saw an example of a mass (a cannon ball) making a closed path in a conservative force field. The potential energy U of a mass m close to the surface of the earth is equal to U = mgh, where g is the gravitational acceleration and h is the height. When the cannon is positioned at height h = 0, the cannon ball starts with potential energy zero, U0 = 0. The work W done by the gravitational field on the cannon ball going upward has two effects: it decreases its kinetic energy—as just discussed—and it increases its potential energy, U1 > U0, so that
- W = −ΔU ≡ −(U1 − U0) = U0 − U1 < 0.
At the highest point, h1, the potential energy is maximum U1 = mgh1 (equal to minus the work performed) and the kinetic energy is zero (this is the point where the motion of the cannon ball changes direction, for a small amount of time its speed is zero). The work done by a conservative force converts a decrease in kinetic energy into an increase of potential energy and conversely:
- W = ΔT = −ΔU, so that ΔT + ΔU = 0.
When the cannon ball dropping down is at height h = 0 again, its kinetic energy is maximum (equal to the energy imparted to it by the exploding gun powder) and its potential energy is zero again.
Example of mechanical work
Work to lift a mass m in the gravitational field of the earth. Close to the surface of the earth, the attractive force is constant and equal to the gravitational acceleration g times m. The work W to lift the mass to a height h is,
When h is positive, and the mass is at rest before and after the lifting (no change in kinetic energy), the work is completely converted into potential energy: U(h) = mgh.
Numeric example:
Here N is the unit newton and J is the unit joule.
Remark
This textbook example seems to contradict energy conservation. Before its lifting, the mass is at rest on the ground with mechanical energy T + U = 0. After its lifting, the mass has still kinetic energy zero, but non-zero potential energy. In other words, its energy has changed during the lifting.
The solution to this paradox is that the agent that does the lifting (a human being, an electric motor as used in elevators, exploding gunpowder, etc.) is left out of the equation. The lifting agent loses at a minimum the energy mgh. (The agent may lose more than mgh because its efficiency may be less than unity; energy may be lost in friction, by incomplete transfer of energy, etc.). The energy of the mass plus the energy of the agent (plus possibly dissipated energy) is conserved.
Secondly, the example seems to contradict the relation W = ΔT (work gives change in kinetic energy), because evidently there is no change in kinetic energy, and yet work has been performed on the mass.
The solution to this apparent contradiction is that the gravitational force Fg must be considered simultaneously with the force Fl exerted by the lifting agent. The two forces work in opposite direction, and apparently |Fl| > |Fg|, otherwise the mass wouldn't go up. However, a net force will accelerate the mass and give it kinetic energy. The solution to this problem is somewhat ingenious. At first the net force is assumed to be small and positive (directed upward) and a small amount of work ΔW is performed, resulting in a small increase in kinetic energy ΔT = ΔW. Once the mass has small speed, the lifting force is decreased so that the net force vanishes, Fl = −Fg. Then the mass pursues its motion upward in accordance with Newton's first law (no net force, no change in velocity). When the mass has arrived close to its endpoint h, the lifting force Fl is decreased to a value just below the gravitational force Fg, so that now the net force performs the work −ΔW that exactly decreases the kinetic energy to zero again. In a very good approximation Fl = −Fg over the whole lifting process and the total work of the net force is
Mathematical formulation
When the force is not constant along the path, or the path is not straight, it is possible to compute the work by infinitesimal calculus. One chooses N + 1 consecutive points on the path
This divides the path in N pieces Δsi, which are small enough to assume that the force is constant, F(ri), on the i-th piece. By their definition as the differences of two vectors, the pieces are straight. The (approximate) total work is obtained by summing the work done along the individual small pieces,
Obviously, when the total path is straight and the force is constant over the path (as in the figure in the previous section), two points give an exact result, i.e., N = 1 suffices.
To improve the approximation one chooses the sampling points ri closer and closer, which makes the pieces Δsi smaller and smaller, so that their lengths go to zero. The limit is the path integral
where we wrote the upper limit (endpoint of the curve) now as r1 (when the number of intervals N goes to infinity, writing the upper limit as rN becomes meaningless).
To show that the work is converted into an increase in kinetic energy, we write for one mass m
where we used F = m a (Newton's second law) and that the acceleration a is the second derivative of r with respect to time. Integrate
where we used that Δs is tangent to the path, i.e.,
Note that from the usual definition of the time derivative of a vector function used here, follows dr ≡ ds and that accordingly the limits in the path integral are r0 ≡ r(t0) and r1 ≡ r(t1). The following important result is obtained that connects the work and change in kinetic energy over the path,
To show that work by a conservative force is converted into decrease in potential energy, we use the relation between force and potential, valid for conservative fields
and by the chain rule
Integrate
In summary,
In total, the conservation of mechanical energy follows
History
The following remarks are based on a paper by Grattan-Guinness.[2]
In 1753 Daniel Bernoulli wrote about "live forces which the man produces during his work". He was close to the statement (proved earlier in this article) that work gives (a change of) kinetic energy (live force).
During the industrial revolution attention of many engineers and scientists became focused on machines (steam engines, waterwheels, windmills, etc.) that were constructed to deliver mechanical work. In that context classical mechanics was seen with fresh eyes and it inspired Lazare Carnot to derive in 1779 a formula for the change in live forces that comes close to the modern equation. It contains the angle between the velocity (ds/dt) and the acceleration (F/m) and integrates over time, hence Carnot's formula is almost (in modern notation):
Next developments came from French physicists and engineers educated at the École Polytechnique, an engineering school which was founded in revolutionary France (1794). Claude-Louis Navier, recognizing energy conservation, derived
where (ξ, η, ζ) is the acceleration of particle with mass m. This is already the modern formula, but not yet the modern terminology. Navier published this formula in 1819, in a new edition of Architecture Hydraulique, an old work (c. 1738) written by Forest de Bélidor. The old work was revised and extended by Navier, (who, parenthetically, referred in it to the 1779 work of Lazare Carnot). As mentioned in the introduction, this work culminated in the formula of the Polytechnician Coriolis: work is path times force.
References
- ↑ G. Coriolis, Du Calcul de l'Effet des Machines, Paris (1829). Also the second edition of 1844 (see Google books) uses the term force vive and not énergie cinétique.
- ↑ 2.0 2.1 I. Grattan-Guinness, Work for the Workers: Advances in Engineering Mechanics and Instruction in France, 1800-1830, Annals of Science, vol. 41, (1984), pp. 1–33
- V. I. Arnold, Mathematical Methods of Classical Mechanics, Springer-Verlag, New York (1978)